Busto di Archidamo III, re di Sparta, considerato come busto di Archimede

I SEGRETI DI ARCHIMEDE

PARTE SECONDA

***

LA MENTE PITAGORICA DI ARCHIMEDE

1* Archimede ragionava come farà Cavalieri con i suoi indivisibili, servendosi altresì del Metodo meccanico, ma anche il Metodo non rivela il segreto delle intuizioni di Archimede, anzi lo nasconde.

C’è un’enorme differenza tra un trattato dimostrativo, perfettamente organato in un apparato di assunzioni, teoremi, enunciazioni, lemmi e corollari, rispetto alle pure e semplici intuizioni, che non potrebbero mai da sole fornire una vera dimostrazione. Le intuizioni sono però i veri semi delle scoperte.

La mente di Archimede sembra continuamente pervasa dalla occulta corrente incessante di un pensiero “produttivo” e “trasformativo”, per cui nella sua intera esistenza non avrebbe fatto altro che dare corpo a un’ispirazione originaria, come appunto avviene per gli artisti.

La Musa di Archimede, così riferisce la tradizione, possedeva qualcosa di divino. Non possiamo condividere le tesi di Julian Jaynes (1976) sul Crollo dellamente bicamerale e l’origine della coscienza (Adelphi, 1996). Scrive Jaynes (pag.100), citando Archimede: L’emozione più forte che l’eroe sente nei confronti di un dio è lo sbigottimento o la meraviglia, il genere di emozione che noi sentiamo quando emerge improvvisamente nella nostra mente la soluzione di un problema particolarmente difficile, o che risuonanell’Eureka!di Archimede nella vasca da bagno. Sulla legge del galleggiamento il racconto fatto da Vitruvio, poi ripetuto da Proclo, è leggendario, e sembra riflettere l’ambientazione tipica delle terme romane.

Il racconto della corona d’oro del re Gerone è un’esemplificazione riduttiva e scolastica di Vitruvio. A questo tema Galileo dedicò il trattato sulla bilancetta. [Con riguardo all’interesse di Galileo per le opere di Archimede rimandiamo in particolare a Ludovico Geymonat e a Stilman Drake].

Le opere di Archimede, a differenza di Platone, nascondono il loro sostrato pitagorico. Esistono però degli indizi, non soltanto di carattere geografico, per ipotizzare in Archimede una discendenza ‘pitagorica’ [ed era questa anche l’opinione degli studiosi Arabi che si interessarono alla sue opere].

Julian Jaynes distingue ad es. il concetto di psyche in Omero, rispetto a ciò si formò in seguito, in direzione dell’anima. Il percorso non è molto chiaro. Ne sarebbe sorto il dualismo tra corpo (soma) e anima (psyche). Questo percorso riguarda Platone.

I pitagorici credevano alla metempsicosi. Nel mito di Er l’arte sublime di Platone recupera l’idea della reincarnazione, che in seguito interessò anche il neopitagorismo romano, di cui Nigidio Figulo fu un grande maestro, con influsso diretto su Cicerone [dal Verbo di Pitagora di Augusto Rostagni, 1924, si può dunque passare al saggio di Jerome Carcopino, 1930, sulla IV egloga di Virgilio].

Il Timeo di Platone è un’opera cosmologica di grande impegno, che non ha volutamente alcun carattere scientifico ed è bensì mitica e profondamente allegorica. Platone era a conoscenza di dottrine segrete, ma preferiva la forma simbolica e dialogica. Socrate è il suo campione, sebbene nel Timeo, accanto a Socrate, si pongano altri tre personaggi: Timeo da Locri (che rappresenta un pitagorico), con Crizia ed Ermocrate (mentre nel dialogo compaiono, accanto a Crizia, il vecchio Solone e i sacerdoti Egiziani).

In età ellenistica circolava uno scritto Sulla natura del cosmo e dell’anima, che era stato fatto passare come il prototipo pitagorico cui si sarebbe ispirato Platone nel Timeo. Il Demiurgo forgiò il Mondo utilizzando dei triangoli elementari. Secondo Platone la geometria è lo specchio ideale della realtà. Gli elementi che compongono l’Universo sono 5 in tutto ed hanno una precisa configurazione spaziale. Sono i 5 solidi pitagorici, le cui “forme” sono le uniche a racchiudere tutto lo spazio in triangoli, qui non considerando la perfezione della sfera, simboleggiante l’Essere di Parmenide o il rotondo sfero di Empedocle (la sfera ha la capacità la forma di racchiudere, a parità di superficie, il massimo volume). I solidi platonici del Timeo sono chiamati: tetraedro, cubo, ottaedro, icosaedro, e dodecaedro. I primi quattro sono associati ai 4 elementi: fuoco, terra, aria, acqua. Cioè i 4 elementi del poema sulla natura di Empedocle di Agrigento, un pitagorico. Il dodecaedro, quinto solido cosmico, rappresentava invece il cerchio delle 12 costellazioni dell’eclittica I 4 elementi di Empedocle, sono però concepiti da Platone in senso atomico, quali semi fondamentali della realtà [non a caso Werner Heisenberg, premio Nobel per la fisica nucleare, con un padre grecista, era innamorato della filosofia di Platone].

Il Timeo fu scritto a tarda età, probabilmente verso i sessant’anni. Proclo attribuisce le 5 figure cosmiche a Pitagora, ma lo scoliasta Suida afferma che il primo a parlarne fu Teeteto, amico di Platone, nato verso il 414 a.C. e figlio di uno dei più ricchi signori dell’Attica. Non si sa se Timeo di Locri sia realmente esistito oppure sia un personaggio inventato da Platone, ma i solidi cosmici derivano sicuramente dalle dottrine pitagoriche. E Platone a queste dottrine si era ispirato.

In un’opera perduta, Archimede studiò anche i 13 solidi semiregolari che completavano l’edificio pitagorico della “stereometria”. Forse non gli fu ignota nemmeno la formula di Cartesio – Eulero che stabilisce la relazione fissa, pari a 2, fra il numero dei vertici, delle facce e degli spigoli di un poliedro. [Leibniz scoprì a Parigi un taccuino di Cartesio, ove il grande filosofo francese aveva annotato tale relazione, senza divulgarla: vedi Il taccuino segreto di Cartesio di Amir D. Aczel, Mondadori, 2006]. La formula dei poliedri è questa: V – S + F = 2. La costante 2 della formula dei poliedri avrebbe un significato dimensionale e rappresenterebbe un invariante.

Cartesio si era posto domande profonde e non aveva voluto divulgare quella formula che aveva ricavato per primo ma che sarà riscoperta autonomamente da Eulero. Cartesio doveva aver meditato su qualcosa che non era riuscito a cogliere. Non si potrebbe spiegarlo diversamente. La grande matematica moderna, funzionale e operativa in tutti campi dello scibile, non ha alcun bisogno di guardarsi all’indietro, tesa com’è in avanti, verso progressive frontiere di sterminata complessità che si di nutrono incessantemente di scoperte e di nuovi linguaggi. Eppure è figlia di idee semplici, sebbene continuamente avvolta nel mistero.

Pitagora riunì insieme il discontinuo numerico e il continuo geometrico, fondendo tra loro la matematica computazione assiro babilonese con la geometria egiziana. Il Mediterraneo non era percorso soltanto dalle navi dei mercanti, ma da pensatori che desideravano altre esperienze e nuovi stimoli.

La civiltà è un aggregato in subbuglio e sommovimento. Certe epoche sono più aperte alle esperienze culturali e geografiche come ad es. il Settecento marinaresco. Fu la stessa cosa per gli inizi della civiltà greca, per vie di terra e di mare. Quella per mare era in genere un’impresa di trasferimento di coloni, di nuove fondazioni e mercati, e si comprende che fosse più pacifica di quelle di terra, che riflettevano spostamenti e invasioni. Il mare Mediterraneo mise in contatto le varie civiltà per millenni. Platone, in tempi diversi, compì almeno tre viaggi in Sicilia, diretto a Siracusa. Qui pretendeva, ma invano, di veder realizzate le dottrine politiche della Repubblica.

Come sappiamo da un passo delle Notti Attiche di Aulo Gellio, Platone andava anche alla ricerca dei libri pitagorici e ne acquistò alcuni a carissimo prezzo. E

Una leggenda fa di Numa Pompilio, primo re storico di Roma dopo i ‘mitici’ Romolo e Remo, un discepolo di Pitagora, artefice del primitivo calendario luni-solare romano, che rimase in vigore fino alla riforma cesariana del 46 a.C.

La fonte di questa leggenda è autorevole: si tratta di Plutarco, grandissimo scrittore, nonché sacerdote delfico. Plutarco è anche la fonte secondo noi più attendibile su Archimede benché scrivesse tre secoli dopo. Che collegamento ci può essere tra Platone e Archimede, e tra Archimede e Pitagora? In che senso la mente scientifica del grande siracusano sarebbe stata quella di un ‘pitagorico’?

2* Non dobbiamo lasciarci condizionare dai pregiudizi perché nell’antichità le scuole di pensiero duravano a lungo negli ambiti geografici in cui erano sorte e si erano sviluppate. Il pitagorismo è un fenomeno che si radicò in Italia e che qui a lungo rimase presente e attivo. Per capire Archimede non basta la sua opera [che difatti genera interrogativi irrisolti, sebbene sia molto bella di per sé]. E non è stato sufficiente nemmeno il ritrovamento del trattato del Metodo per chiarire gli interrogativi. C’è un lato oscuro di Archimede, riguardante la sua genialità e le sue stesse forme di pensiero, che si sottrae a indagini di tipo ordinario. Sfidare Archimede come persona concreta, esistita ed operante in un dato ambiente, è un passo necessario per comprenderlo meglio anche come scienziato. Gli Studiosi moderni guardano alle opere, ma forse dimenticano l’uomo che le ha composte. Poi notano con meraviglia che Archimede poteva essere stato persino un burlone, che produsse falsi enunciati ai danni dei matematici alessandrini e cercano una giustificazione psicologica rispetto a quella che invece poteva essere stata una sfida oppure lo smascheramento di matematici presuntuosi che si vantavano di capacità che non possedevano.

Gli Studiosi di Archimede si rendono perfettamente conto dell’enormità inutile del famoso “problema bovino”, che i matematici moderni hanno risolto anche con l’ausilio del computer, ma lo considerano un omaggio a Eratostene, mentre il geniale epigramma matematico in 44 versi, implicitamente ironico e polemico, ben poteva rappresentare un bando di sfida o meglio ancora una raffinata forma di vendetta con un insegnamento morale. Non dobbiamo scordare che Archimede era il “Signor Alfa”, mentre Eratostene era chiamato il “Signor Beta”. Tra i due personaggi, Eratostene era più giovane di Archimede, a un certo punto potevano essere sorti gravi ragioni d’attrito, e noi crediamo che fu proprio così. Tra l’altro, la struttura matematica della seconda parte del problema dei “buoi del sole” (che si ispirava a un brano dell’Odissea), si rifà ai numeri triangolari e quadrati che sono uno specifico portato delle concezioni pitagoriche. I numeri triangolari sono dati dalla somma dei numeri naturali consecutivi, a partire dall’unità. Il primo numero triangolare è 3 = 1 + 2. Il secondo è 6 = 1 + 2 + 3. L’altra loro caratteristica è che possono essere rappresentati visivamente in forma di triangolo, come una scala a pioli. Il triangolo è in continua crescita. In algebra la formula dei numeri triangolari è n (n + 1)/2. I numeri quadrati, cioè i numeri della forma n per n, sono la somma di due numeri triangolari successivi: es. 3 + 6 = 9 = 3 per 3; 6 + 10 = 16 = 4 per 4.

Come stanno le cose? Siamo costretti a immaginare [come diceva lo storico francese Geogers Duby]. Quando si avverte la presenza di qualche anomalia, e mancano i documenti storici di supporto che la giustifichino, immaginare non è vietato. Ed è quanto dovrebbero fare gli storici per arrivare a capire meglio il genio di Archimede.

Se il filosofo della scienza Karl Popper ha dedicato a Parmenide di Elea una formidabile serie di saggi, poi raccolti in un volume, trattando in quest’ambito persino della teoria della relatività di Einstein, al pensiero iniziatico di Empedocle di Agrigento ha dedicato, nel 1995, un saggio Peter Kingsley, i Misteri e magia nella filosofia antica – Empedocle e la tradizione pitagorica.

Elea e Agrigento erano sede di gruppi pitagorici. Di formazione pitagorica furono Parmenide ed Empedocle. La scuola pitagorica in Italia rappresentava la continuità storica del sapere scientifico e filosofico. Archimede nel III secolo a.C. ne fu il frutto più splendido. Il nucleo intuitivo delle opere di Archimede conserva un’impronta pitagorica, sebbene le nostre conoscenze su Pitagora, ovviamente frammiste a leggenda, debbano essere desunte da fonti tarde e assai discutibili, come ad esempio Giamblico. L’impronta mitica della figura di Pitagora ne attesta tuttavia l’importanza e l’incisività. Archimede pitagorico non appartiene al regno della fantasia, essendo la chiave d’accesso per la comprensione intima della originalità del suo pensiero scientifico-matematico, in ambito italico, distinto da quello di tipo ellenistico ovvero ‘allessandrino’.

3* Archimede non era uno scienziato entrato nell’orbita dell’atomismo ionico, divenuto epicureo; ma era un pitagorico della scuola italica, e, dunque, anche un matematico platonico. Quest’affermazione ha un peso decisivo per la comprensione di Archimede e delle sue opere che presentandosi attraverso impeccabili dimostrazioni, capaci di esaurire ogni spazio al loro interno, sembrano però provenire dal nulla, almeno nel senso che Archimede dimostra perfettamente, ma non spiega mai come facesse a sapere già prima ciò che dimostrerà dopo. Nella matematica moderna il requisito essenziale è quello della coerenza di sistema. Domina il formalismo logico. Si tratta di giochi raffinatissimi, che procedono da enti fondamentali, per i quali non occorre alcun legame con la realtà concreta, salvo scorgerne in seguito la sua irragionevole efficacia in fisica e nelle scienze applicate. La matematica è arte raffinata del pensiero astratto. Ma così non era per Archimede, sebbene sia stato definito,e a buona ragione, come il padre della scienza dell’età moderna e della matematica del calcolo infinitesimale. Paradossalmente è così.

L’impostazione formale delle opere di Archimede, che sono dei gioielli del pensiero, è perfettamente coerente ed è sistemata in modo esemplare, come già fece per primo Euclide (di cui si dice che furono suoi successori nel Museo di Alessandria dapprima Conone e poi Dositeo, amici di Achimede).

L’arte dimostrativa archimedea si presenta in ragionamenti impeccabili, ma ciò non toglie che sia necessario cercare di comprendere cosa ci fosse sotto. Attilio Frajese, traduttore italiano di Archimede [non molto apprezzato da Napolitani], si domandava – a buona ragione – da dove il Siracusano avesse potuto trarre certi “numeri” o “rapporti semplici” che caratterizzano i suoi risultati. Lo stesso Stomachion [insieme al Metodo] pone simili domande: “Come ragionava Archimede”? E com’era possibile che nell’antichità ci fossero già dei rudimenti di calcolo combinatorio?

Secondo Plutarco, Senocrate (396-314), discepolo di Platone e suo compagno di viaggio in Sicilia, aveva calcolato il numero delle sillabe che potevano essere formate con le lettere dell’alfabeto greco, giungendo allo strabiliante risultato di oltre mille miliardi. Si è scopeto di recente che sempre Plutarco aveva fornito importantissime notizie riguardati i numeri di Ipparco, che tornano in ballo per la comprensione degli ‘scopi’ dello Stomachion.

E come fece Archimede a proporre a Eratostene e ai (boriosi) matematici alessandrini della sua cerchia – e soprattutto perché – quel terribile problema bovino, composto in forma epigrammatica, pieno di allusioni letterarie, che partendo da Omero arrivano fino a Platone e alle Argonautiche di Apollonio Rodio?

Archimede, oltre la sua leggenda, rimane alquanto misterioso. Nelle sue opere convivono in perfetta armonia arte e scienza, bellezza e ordine; ma non tutto quanto giunge immediatamente in risalto. I trattati archimedei sono belli ma anche laboriosi e complicati. Non si riesce a capire bene quale opera preceda l’altra, si ha quasi la sensazione che tutto stia insieme, ma questo enorme capolavoro in fondo si basa su qualcosa che è semplice ed è però sfuggente. Potremmo ricorrere al paragone tra un piccolo seme e una grande pianta. Quest’analogia contiene in sé il mistero vitale dell’input assai più modesto dell’output, e con un senso dobbiamo dire di profonda meraviglia, che attiene al fascino straordinario di un personaggio mitico quale egli fu anche per i suoi contemporanei. Il signor Archimede, lui era l’Alfa, era il primo in tutto.

Una posizione di primazia e di grande fama che Archimede doveva aver raggiunto in età ormai matura e che lo vedeva contrapposto nel suo splendido isolamento nella natia Siracusa alla boria accademica professata dagli scienziati alessandrini al tempo trionfale di Eratostene che matematico vero non era e che tale non poteva nemmeno essere: grande filologo, sì; e geografo, mitografo, tuttologo, e persino scienziato. Ma è da ritenere che la sua fama di eterno secondo, cioè di Signor Beta, stesse piuttosto a significare che la sua abilità di filologo gli aveva permesso sopratutto di recuperare e di rielaborare antichi segreti depositati nell’immensa biblioteca di Alessandria, capeggiando un nutrito gruppo di specialisti, matematici e scienziati, aggregati al Museo.

I laboratori culturali di Alessandria erano un’officina assai organizzata, con tanti addetti, e non una bottega artigiana della scienza, come doveva essere per Archimede a Siracusa, in una posizione analoga a quella che poi sarà la condizione di Leonardo da Vinci o di Galileo Galilei.

4* Archimede non aveva un carattere accomodante, ma non era nemmeno troppo serioso: si potrebbe definirlo burbero, ma anche giocoso e burlone (R. Netz), e si dovrebbe aggiungere che sapeva ben distinguere gli amici di valore dalle mezze tacche che negli ambienti scientifici di Alessandria, corrotti dal potere, non dovevano mancare (lo testimonia anche un epigramma riportato da Ateneo).

La personalità di Archimede era caratterizzata da assoluta competenza e da nobilissimo rigore. E’ pressoché inconcepibile la presenza di un personaggio come Archimede ad Alessandria in quel periodo. Continuava a inviare le sue opere ai suoi pochi amici alessandrini, che riducevano alla ristretta cerchia dell’amico Conone, grande astronomo e matematico provetto, probabilmente appartato a Canopo con i suoi pochi collaboratori. Tra Siracusa e Alessandria regnavano proficui scambi economici e commerciali, ma erano modi diversi. Alessandria era cosmopolita, mentre Siracusa era stata una antica colonia greca d’illustri tradizioni. Teocrito da Siracusa si recò ad Alessandria, mentre la presenza di Archimede nella capitale tolemaica riguardò soltanto la giovinezza.

E’ vero o è falso che il metodo “per esaustione” inventato da Eudosso [il profilo biografico di Eudosso ci è stato tramandato da Diogene Laerzio nelle Vite dei filosofi: egli fu un collaboratore assai capace di Platone, che Archimede molto apprezzava come matematico], anticipò il calcolo infinitesimale dovuto a Fermat, e poi a Newton e a Leibniz? E’ vero che senza la grandezza piccola a piacere di Archimede il calcolo infinitesimale non poteva essere concepito?

In che rapporto si trovano la civiltà ellenistica dei tempi di Archimede e la rivoluzione scientifica moderna nel XVII secolo? ‘Antico’ non è ‘moderno’. E’ necessario fare la tara. In che misura il moderno proveniva dall’antico, stando alle ammissioni personali di un grande protagonista della rivoluzione scientifica moderna come Newton che affermava di essersi arrampicato sulle spalle dei giganti?

La matematica del movimento, lo spazio e il tempo correlati alle variazioni e agli infinitesimi, gli antichi non l’avevano immaginata. La loro geometria era statica, apparteneva concettualmente all’Essere di Parmenide, sebbene Platone avesse introdotto il punto senza dimensioni. Né la fisica antica aveva mai concepito una dinamica. L’universo platonico delle forme o archetipi, tal quale l’Essere di Parmenide, era idealmente immobile. L’immutabilità della verità impediva di legarsi troppo a fenomeni spuri e transitori.

La convergenza all’infinito di serie opposte verso un limite definibile con approssimazione infinita, insieme allo stesso concetto di grandezza “piccola a piacere”, non rappresentavano per Archimede nulla di speciale, aldilà dalle esigenze della sua ricerca. Anche l’utilizzo da parte di Archimede dell’infinito potenziale [che secondo Reviel Netz sarebbe un’anticipazione dell’infinito attuale moderno], rispondeva a ragioni proprie. Archimede se ne serviva per superare l’ostacolo del curvo. Invece le reminiscenze pitagoriche, l’influsso platonico, le valutazioni dimensionali e una teoria simile a quella degli indivisibili di Bonaventura Cavalieri [che nel Metodo comportava esperimenti meccanici], gli permetteva di intuire in anticipo certe soluzioni e di procedere in seguito alle rigorose ed esaurienti dimostrazioni.

I misteri di Archimede sono molteplici. Riguardano le realizzazioni pratiche (ad es. la famosa sfera celeste) fino ad arrivare al segreto della sua formidabile intuizione (geometrica, matematica e meccanica).

Una possibile spiegazione di questa genialità, che raggiunse i vertici ma che non era nemmeno un frutto isolato, proveniente dal nulla, si può rintracciare ipotizzando che Archimede fosse l’epigono della scuola italica d’impronta pitagorica, che aveva già dato geni come Parmenide di Elea ed Empedocle di Agrigento, come Filolao di Crotone e Archita di Taranto [tanto per citare i nomi maggiori a prescindere dal campo di attività]. Era, quella italica, una scuola di grande ispirazione, il cui più ambizioso obiettivo consisteva o era consistito nella comprensione matematica dell’Universo in termini razionali e geometrico numerici, in base alle regole analogiche dell’armonia musicale e a principi di bellezza che si contenevano nelle leggi di proporzione, ma anche di equilibrio, di conservazione e d’immutabilità. L’Essere è statico per eccellenza. Il divenire nel tempo è mutevole e caotico. Il logos non poteva ammettere l’irrazionalità, e se questa si manifestava, come nel rapporto irriducibile tra il lato e la diagonale del quadrato, ciò non era la prova del caos, ma di un ordine superiore, inerente all’Essere stesso. Il numero era granulare, la geometria era continua.

Le “dicotomie pitagoriche” rientravano nei problemi stessi dell’Essere, come tale, e non ne costituivano, al contrario, aspetti irrazionali, contraddittori e compromettenti. I pitagorici ne erano consapevoli, niente affatto turbati. L’essenza del quadrato consisteva nel lato e nella diagonale. La geometria completava l’immagine dell’Universo numerico. Non c’è alcuna frattura tra il pensiero pitagorico e il successivo pensiero di Platone.

5* Filolao di Crotone era stato un eccellente cosmologo. Archita di Taranto era un valentissimo matematico e un provetto meccanico, inventore di strumenti meccanici e di curiose realizzazioni, autore anche di un trattato sulla musica. Erano dei capiscuola in certe aree geo-politiche della Magna Grecia in cui non mancava una classe dirigente colta a prescindere dalle questioni di potere. Le grandi istituzioni culturali di Alessandria – il Museo e la Biblioteca – riflettevano su scala più ampia e organizzata quanto in precedenza esisteva ad Atene, con l’Accademia di Platone e il liceo di Aristotele, ma anche in Italia, a Crotone, al tempo di Pitagora.

La collaborazione di Archimede con gli ambienti scientifici di Alessandria nel periodo di massima fioritura delle scienze sotto Tolomeo II Filadelfo e poi Tolomeo III Evergete, trova spiegazione non soltanto nel fatto che Archimede aveva soggiornato in Egitto per un certo periodo svolgendovi varie attività, ma altresì come apporto che dall’ambiente italico si era riversato a Siracusa, nuova patria della ricerca scientifica finanziata dai regnanti., in particolare da Gerone. Archimede “pitagorico” è il trait d’union tra i bagliori del mondo italico di Pitagora e il mondo scientifico alessandrino al suo apogeo. Se si prescinde da questo quadro, molte cose diventano incomprensibili, rimanendo senza un supporto. Infine si può comprendere che il campo dei ritrovati scientifici di tipo applicativo era limitato, in specie per Siracusa, al settore navale e alle macchine militari di tipo difensivo. L’astronomia rimaneva la scienza regina, accanto alla matematica e alla geometria. Archimede, figlio di un astronomo pitagorico, era pure lui un valente astronomo. A sua volta l’astronomia e la geometria erano i supporti scientifici dell’arte pratica della navigazione e della geografia. I ritrovati di Archimede vertevano anche in ambito agricolo (irrigazione) e nel settore minerario (bonifica delle miniere da infiltrazioni d’acqua). La scienza antica, non pressata da esigenze pratiche, rimaneva essenzialmente teorica e speculativa. Ciò che l’esperienza aveva suggerito come strumento idoneo (leve, argani, pulegge ecc.), adesso trovava una sistemazione nei principi teorici inerenti (non il viceversa, se non per qualche invenzione, come la coclea da irrigazione, per il sollevamento dell’acqua del Nilo).

6* Corrispondente privilegiato di Archimede era stato Conone. Non sappiamo bene quali opere Archimede gli avesse inviato, e sicuramente gliene mandò. In seguito, dopo la morte prematura di Conone, corrispondenti del Siracusano furono gli allievi di Conone, Dositeo di Caulonia [città greca della Calabria: ma si preferisce riportare Dositeo a Pelusio, luogo dove lavorava e alle sue ascendenze ebraiche] e il matematico Zeusippo, al quale Archimede aveva inviato un trattato sui numeri prima del 240; ma anche Eratostene di Cirene, quanto al trattato sul Metodo meccanico e al terribile “problema bovino”.

Che cosa riceveva a sua volta Archimede da Alessandria? Dovremmo presupporre una condizione bilaterale, ma possiamo trarci all’impaccio ipotizzando che Archimede sembrava uno che invia opere, ma non ne riceve, eccezion fatta per i rapporti con l’amico Conone.

E’ certa la collaborazione scientifica con Conone, l’unico in grado comprenderlo. E se Archimede lo rimpiange con note accorate vuol dire che Conone era una figura eccezionale, meritoria di dirigere la Biblioteca o il Museo, che poi facevano tutt’uno. Conone lavorava a Canopo e non sembra che abbia mai avuto grandi incarichi sebbene fosse famoso. Ciò era dovuto alla sua scienza, non al grado di potere raggiunto a corte.

Tali contatti di Archimede, nelle lettere di prefazione e d’accompagnamento delle opere, appartengono a un periodo successivo alla morte di Conone che nel 246 a.C. doveva essere ancora in vita. Sorge una serie di problemi: cosa aveva fatto Archimede prima di arrivare a quarant’anni; cosa precede cosa; e quali sono le opere che lui considerava fondamentali; perché scrisse il Metodo, oppure viceversa perché lo tenne nascosto, e poi lo inviò a Eratostene, e se glielo mandò su sua richiesta o motu proprio, e quando (ritengo in epoca non lontana dalla morte di Conone).

Eratostene non era un matematico paragonabile a Conone e ad Archimede. Era un letterato, anche se si occupava di matematica e di scienza. Sappiamo abbastanza di Eratostene, ma poco resta delle sue opere. Pochissimo sappiamo di Conone, quasi nulla di Dositeo, suo affezionato allievo. Archimede e Conone dovevano essere coetanei. Probabilmente si erano conosciuti ad Alessadria, al Museo, e qui avevano stretto amicizia.

Secondo Reviel Netz, il nome “Dositeo” era comune agli ebrei alessandrini perché si tratta della traduzione greca dell’ebraico Matityahu, ovvero Matteo. Avrà ragione Netz. Secondo noi, Dositeo era originario dall’Italia ed è questa la ragione per cui Archimede si fida di lui, nell’inesausta memoria per l’amico Conone. E Dositeo doveva essere un ottimo astronomo e matematico, miglior allievo di Conone, il quale ultimo aveva fatto osservazioni anche in Italia, come sappiamo da un commentatore di Tolomeo. Dositeo poteva essere una conoscenza diretta di Archimede ed è possibile che tutti e tre – Archimede, Conone e Dositeo – abbiano lavorato insieme intorno a certe osservazioni che consistevano nella possibilità della determinazione della longitudine col metodo astronomico nelle eclissi di luna. Ciò tornava utile per la navigazione in alto mare e per tutte le questioni geografiche. Non s’inviano importanti e innovativi trattati matematici a qualcuno che non si conosca bene, di cui ci si fidi, se non c’è stata una relazione diretta e una conoscenza, e se soprattutto non c’è un preciso scopo scientifico condiviso. Archimede era estraneo agli ambienti della Biblioteca e del Museo ad Alessandria, ma era legato a Conone e a Dositeo. Ciò significa che la scuola di Conone non aveva molto a che fare col resto. La fama di Conone riposava sulle sue qualità che dovevano essere umanamente e intellettualmente simili a quelle di Archimede. Lo studio del cielo era legato alla geometria. Archimede e Conone erano astronomi e matematici.

7* Polibio, grande storico romano d’origine greca, abbastanza vicino ai fatti che descrive, conferisce certezza assoluta alla strenua difesa di Siracusa con i terribili ritrovati di Archimede. Gli specchi ustori sono una favola inventata da Tzetze? Tito Livio, che si sofferma a lungo sul saccheggio di Siracusa, è invece assai parco di riferimenti sui ritrovati di Archimede, che sarebbero stati catapulte e grandi balestre. Lo smacco militare subìto dal console Marcello dotato di potente esercito di terra e di una grande flotta andava ovviamente coperto dagli storici roman, dal momento che Siracusa cadde soltanto per tradimento. La reticenza di Livio rispetto alla realtà effettiva delle cose riguarda anche la morte di Archimede quasi sicuramente eliminato dai Romani per vendetta.

Le fonti sono piuttosto tarde, sebbene ad Archimede faccia riferimento Polibio nella storia delle guerre puniche, composta sotto la protezione dei due figli di Paolo Emilio, Fabio Massimo Emiliano e Cornelio Scipione Emiliano [la distruzione di Cartagine avvenne nel 146 a.C.]. Nell’ambito del circolo degli Scipioni trovano la loro collocazione alcune notizie che ci sono giunte sulla realizzazioni meccaniche di Archimede, come ad esempio la famosa sfera celeste. Il genio del Siracusano spaziava in molti settori, ma anche questi interessi depongono per la sua appartenenza alla scuola italica d’impronta pitagorica.

LA SFERA CELESTE E IL PADRE DI ARCHIMEDE

1* La sfera celeste costruita da Archimede, che fu sicuramente predata dai romani durante il sacco di Siracusa dopo la conquista del console Marcello (benché le fonti non ne parlino direttamente), venne dapprima conservata nella casa di Scipione Emiliano, per finire poi appesa nel tempio di Vesta, dove appunto la notò Ovidio, mentre Cicerone tace tale importante dettaglio. Così si esprime Ovidio, il poeta di Sulmona amico di Properzio, a proposito della sfera celeste costruita da Archimede: Arte Syracusia suspensus in aere clauso / stat globus immensi parva figura poli (sesto libro dei Fasti, a proposito del culto di Vesta, dopo aver riportato le celebrazioni per la dea Mente, sicuramente connessa alla radice -Mens, che è poi la stessa di Mnerva etrusca, con un significato lunare). La sintetica descrizione di Ovidio va interpretata.

Il poeta elegiaco del quarto secolo d. C., Claudio Claudiano, di probabili origini egiziane, dà invece un’altra descrizione, che è molto più diffusa e che si aggiunge a quella già data per primo da Marco Tullio Cicerone.

Cicerone stesso, in un frammento della Repubblica, che si riferisce al sogno di Scipione, descrivendo il cielo e l’armonia dei pianeti, sembra implicitamente rifarsi a un planetario. Cicerone poteva aver avuto presente sia l’Arenario che la sfera celeste di Archimede conservata a Roma; ma nessuno di questi autori riesce a descrivere con precisione in che cosa consistesse questa meravigliosa “sfera”.

Poteva essere un planetario in miniatura di tipo meccanico, con ingranaggi di bronzo e racchiuso in una sfera di vetro? Mosso da che cosa?

Claudiano, che nei suoi versi descrive efficacemente la “sfera celeste” di Archimede come se appunto l’avesse osservata da vicino e ancora funzionante, lascia intendere che la luna orbitava intorno alla terra, e che la terra era posta al centro del planetario. Il planetario era poi di tipo piano oppure consisteva in una sfera?

Claudiano parla di un “piccolo globo”, che probabilmente doveva essere di vetro. All’epoca di Archimede erano stati già inventati i meccanismi a molla, con ruote munite di differenziale, come appunto sarà anche nel caso del meccanismo celeste o strumento in ingranaggi di bronzo ripescato in mare ad Antikytera. Oppure il planetario di Archimede o modello dei cieli era mosso per mezzo di unmoto uniforme dell’acqua, secondo quanto è riportato per le sfere celesti nella Collezione matematica di Pappo (VII, 2) che è una delle fonti più importanti su Archimede? Archimede costruì più modelli di sfera celeste?

Se Archimede si fosse ispirato a Filolao o ad Aristarco avrebbe dovuto porre il sole al centro del modello meccanico. Del resto, anche il cosmo pitagorico era eliocentrico. Secondo la descrizione di Claudiano in questo planetario il finto sole misurava l’anno e la luna ritornava al suo mese. Ne riparleremo.

2* Certi segreti sembrano attraversarne la vita e l’opera. Il mistero Archimede è un giallo affascinante, destinato a concludersi con un omicidio sicuramente non occasionale. Senza un tradimento interno, Siracusa non sarebbe mai caduta, vivo Archimede, in mano ai Romani. Il siracusano poteva anche non essere, a quel tempo, così vecchio, come afferma Tzetze, sebbene ciò sia confermato anche da Polibio. Dipende dalla data di nascita, che ignoriamo. Si pensa che sia nato verso il 287 a.C., per cui nel 212, anno della morte, avrebbe avuto circa 75 anni. La data di nascita è attenibile rispetto alla presumibile data di morte del grande amico Conone. Ed è un Archimede “pitagorico”, così ricordato dagli Arabi, che preferì restare in patria e che si considerava abbastanza estraneo all’ambiente alessandrino del Museo e della Biblioteca.

Il neoplatonico Giamblico scrisse nel IV secolo d.C. una Vita pitagorica, opera fondamentale ma leggendaria, alla quale accluse il catalogo dei pitagorici e delle donne pitagoriche in Italia, città per città. Si pensa che il catalogo di Giamblico sia da attribuire ad Aristosseno di Taranto, vissuto nel IV secolo a.C. Tale catalogo, che annovera Parmenide, Empedocle, Archita, Filolao e molti altri pitagorici noti e meno noti, potrebbe però provenire dagli ambienti stessi dell’Accademia ed essere stato compilato qualche decennio dopo la morte di Platone, avvenuta nel 348 o 347 a.C.

Nell’elenco dei pitagorici di Siracusa leggiamo tre nomi soltanto: Leptines, Phintias, e Damon. A interessarci è il secondo nome: Pinthias, cioè “Fitia” (e non Fidia). In un passo dell’Arenario – opera cosmico-numerica dedicata da Archimede a Gelone e perciò databile verso il 240 a.C. (quando Archimede poteva avere all’incirca l‘età di 47 anni), ritenuto però corrotto a causa di un errore di trascrizione, leggiamo in greco: Pheidia tou akoupatros. Il fatto saliente è che non esistono nomi di luoghi, o di persona, che siano “Acupatro”. Ma se mutiamo il k in una m, leggeremo Pheidia toumou patros, cioè “Fidia mio padre”.

Con questa lettura, proposta nel 1883 dal grande filologo tedesco F. Blass, verremmo dunque a sapere direttamente da Archimede (la cui data nascita può collocarsi intorno all’anno 287 a.C.), che l’astronomo “Fidia” era “suo padre”. Pheidia però non è Phintias. Ma si potrebbe ugualmente supporre che la trascrizione sia stata alterata anche nel nome proprio (doppio errore del copista o del copista del copista), per cui il nome vero del padre di Archimede non sarebbe stato Fidia (come il grande scultore ateniese), ma Fintia (nome proprio nella Siracusa dorica).

Tale conclusione è legittima. Come era stato alterato il seguito della frase, nel senso di “Fidia figlio (di un inesistente) Acupatro”, la vera frase di Archimede – intelletto divino come dissero Cicerone e Plutarco – doveva essere invece “Fitia mio padre”. E questo “Fitia” sarebbe quel pitagorico dell’antico elenco post platonico, utilizzato da Giamblico senza rendersi conto che “Fitia” era anche il padre di Archimede.

I nomi degli ultimi pitagorici figuravano in un catalogo dell’accademia che era stato aggiornato anche sui viventi di grande fama. Questo Fitia sarebbe stato perciò attivo, a Siracusa, all’inizio del III secolo, quando la sua fama era ormai giunta all’apice. Era poi ben degno del valentissimo astronomo Fitia il nome sublime impartito al figlio: Archimede, “primo nell’intelletto” (un genio figlio di un altro genio).

Tuttavia, perché Giamblico non fece alcun riferimento ad Archimede e non chiarì o aggiunse, che quel pitagorico di Siracusa era il padre (astronomo) di tanto figlio? Il motivo dell’omissione sarebbe dipeso dal fatto che all’epoca in cui Giamblico scriveva, basandosi su un elenco molto più antico, risalente a qualche decennio dopo la morte di Platone, Archimede era ancora un bambino, e dunque la sua futura fama e la sua gloria non erano ancora sorte.

Fitia di Siracusa doveva essere un astronomo pitagorico così importante e già famoso da lasciare da giovane grande impressione nei suoi contemporanei. La sua fama era giunta ad Atene, negli ambienti dell’Accademia, dove aveva militato un altro astronomo e grande matematico, Eudosso. Il compilatore del catalogo lo inserì accanto ad altri due nomi, ma non in ordine alfabetico. Si trattava di un ordine cronologico? Ci sono, nello stesso catalogo, dei pitagorici tra loro contemporanei. L’elenco è casuale, e non risponde ad alcun criterio interno.

Il nome “Fitia” – trasformato dal copista, per errore o forse per intenzione, in “Fidia” – è accostato nell’Arenario a quello di Eudosso, in una successione a discendere che giunge fino allo stesso autore, Archimede, astronomo pure lui, almeno nel periodo della sua giovinezza. Ed è perfettamente coerente il ricordo del padre di Archimede in questo contesto dell’Arenario, tanto più che il giovane Gelone veniva, in quel momento associato, al trono da Gerone II, suo padre.

Archimede dice: colui che fu di me il padre. Fidia (secondo noi Fitia) era un astronomo contemporaneo ad Aristarco, che era stato allievo di Stratone di Lampsaco.

Eudosso aveva misurato il diametro del sole rispetto a quello della luna [quindi ne aveva stimato anche le distanze che nell’antichità erano però totalmente errate per questioni tecniche], e queste misure fatte da Eudosso erano state poi aggiornate dal padre di Archimede, e in seguito da Archimede stesso, sempre a Siracusa. La fama pitagorica di Fitia si era dunque prodotta in vita, accanto a quella di Eudosso, noto platonico. L’elenco pitagorico utilizzato supinamente da Giamblico non era soltanto un catalogo di morti.

Ecco spiegato perché gli Arabi dissero che Archimede era “figlio di Pitagora”. Non solo Archimede era un “pitagorico”, ma “pitagorico” era stato anche suo padre.

La scuola pitagorica della Magna Grecia nel III scolo a.C. era giunta ai suoi ultimi esponenti di rilievo per una sorta di esaurimento politico delle sue aree geografiche. I Romani premevano da nord e il mondo alessadrino aveva fondato la sua nuova scuola ad Alessandria. Archimede pitagorico, fiorito a Siracusa quale rampollo di uno degli ultimi grandi pitagorici, volle rimanere a Siracusa con i suoi pochi allievi. Non lo allettava il mondo ellenistico che aveva finito per attrarre anche il grande poeta Teocrito. Archimede rimaneva quell’ingegnere capo, tanto stimato da Gerone II, il vivace tiranno di Siracusa, ed era, proprio lui, l’ultimo ‘caposcuola’ del pitagorismo italico. Il Re Gerone II aveva ambizioni scientifiche e teneva alte le sorti economiche e commerciali di Siracusa come potenza navale. In una età difficile per le colonie greche, per via dei Cartaginesi, sempre attivi nel Mediterraneo, e per via dei Romani che oramai stavano dominando l’Italia e che presto avrebbero avuto con le loro flotte anche il dominio sul mare. Archimede era un punto di riferimento e una gloria per la sua Patria.

LA GRANDENAVE SYRAKUSIA

E LA MERIDIANA DEL TEMPIO DI ATHENA

1* Cicerone, grande neopitagorico romano, definì Archimede umilem homunculum, mentre Silio Italico usò l’espressione nudum opus – cioè spoglio di ricchezze – così ingenerandosi l’idea che fosse di povera famiglia. Ciò è falso. E’ probabile che Archimede fosse imparentato col tiranno di Siracusa Gerone II.

Gerone era un capopopolo di casta militare e d’estrazione nobiliare, salito al potere nel 275, e aveva anche velleità ingegneristiche, oltre che politiche. Infatti, fece costruire (verso il 269 a.C.) una grande nave, la Siracusa, subito destinata a suscitare l’ammirazione e l’emulazione di Tolomeo II Filadelfo, e di cui favoleggiò alcuni secoli dopo, ma a buona ragione, Ateneo, all’epoca dell’imperatore Commodo, nei Sofisti a banchetto, riprendendone ampie notizie da un libro perduto di Moschione (un autore d’età alessandrina).

Se con mano femminea – cioè senza sforzo – gli strumenti meccanici di Archimede potevano trascinare una pesante nave a riva (operazione pratica molto importante), ecco in breve la descrizione della grande nave Syrakusia, alla cui progettazione avrebbe attivamente partecipato il giovane Archimede.

Questa nave possedeva una stazza di 4200 tonnellate. Si sviluppava in altezza su tre ponti, con quaranta lussuose cabine; sul terzo ponte c’erano otto torri fortificate contro gli attacchi dei pirati, una biblioteca, un bagno, e un tempietto dedicato ad Afrodite. Mosaici ovunque, e camminamenti protetti dal verde di alberi da frutto e da pergolati, con una catapulta con una gittata di oltre uno stadio, che era stata progettata da Archimede.

La grande nave non era mossa soltanto dai remi, disposti in tanti ordini, ma dalle vele: aveva tre alberi e l’albero maestro era stato ricavato da un pino gigantesco. Una tale nave non era facilmente manovrabile. Era piuttosto un monumento marittimo, che una nave adatta alla navigazione di spola tra Siracusa e Alessandria.

Tolomeo III, detto l’Evergete, volle imitare Gerone II, costruendo una nave da guerra di oltre 6.000 tonnellate, lunga 124 metri e alta 21, formata da due scafi appaiati, con un ponte capace di contenere circa 3.000 soldati. Non contento di ciò, l’Evergete si fece costruire una Seconda nave di 90 metri di lunghezza, 14 di larghezza e 20 di altezza, che ormeggiata sul Nilo, fu adibita ai banchetti di corte [le navi romane del lago di Nemi erano notevolmente più piccole].

Siracusa era una grande città marinara che in prevalenza esportava grano. La ricchezza della città è certificata dal grande bottino che vi fecero i Romani, portando a Roma anche la meravigliosa “sfera celeste” di Archimede, che quale aveva progettato e realizzato anche una grande meridiana.

Sul luogo più elevato dell’isola di Ortigia, davanti alla città, sorgeva un tempio dedicato ad Atena-Minerva che secondo Diodoro Siculo era stato costruito nel V secolo. Rivolto a oriente, sulla sommità di questo tempio risplendeva uno scudo d’oro, segnacolo ai marinai. Sul pavimento del tempio Archimede aveva tracciato una meridiana solare, completandola con la linea equinoziale. Il sole nascente attraversava le aperture del tempio di Atena e penetrando le porte del più antico tempio di Giove, risalente al VII secolo, finiva col disegnare un disco solare nella montagna di rimpetto (i Colli Iblei).

Viceversa, al tramonto, sull’orizzonte orientale. Questa tradizione, priva di riscontri nelle fonti storiche, ebbe tuttavia un’eco nel 1576, per la riforma del calendario sotto Gregorio XIII, e di nuovo nel 1766, quando l’Accademia delle Scienze di Parigi inviò a Siracusa l’astronomo Chabarai (P. Midolo, Archimede, 1912).

Il discorso si allarga nuovamente al rapporto tra antico e moderno per quanto riguarda il grande intervallo che divide le due epoche: quella di Archimede e quella della rivoluzione scientifica. Ma abbiamo già visto attraverso alcuni esempi tecnologici che l’epoca ellenistica aveva raggiunto un sorprendente livello di modernità per poi spegnersi nei secoli a venire sotto il dominio romano.

2*La caratteristica generale più certa della tradizione scientifica europea è che essa consiste in una serie di note aggiuntive ad Archimede (così Reviel Netz, in analogia a quanto avvenne in filosofia nel caso di Platone).

Netz esagera giacché Archimede è e rimane un autore antico e anche perché la scienza moderna da Galileo in poi fu tutt’altro in termini sociali e di costume (oggigiorno la scienza è un’impresa collettiva, anche se le rivoluzioni radicali finiscono per rimanere atti individuali, al contrario di quanto avviene in politica).

I Discorsiintorno a due nuove scienze, pubblicati da Galilei nel 1638, quando Archimede era morto da 1850 anni, hanno un grande debito nei confronti del Siracusano. Un debito che fu ampiamente riconosciuto da Newton, il quale disse che si era “arrampicato sulle spalle di giganti”, intendendo per tali I grandi antichi tra cui Pitagora e Archimede. La rivoluzione scientifica del XVII secolo sarebbe figlia (tardiva) di quella avvenuta già venti secoli prima, in età alessandrina. Tale debito andrebbe riconosciuto, in linea di principio, e non in termini diretti, ai grandi scienziati ellenistici. Il patrimonio scientifico antico andò perduto. Roma conquistò il Mediterraneo, ma non seppe conservare e trasmettere ciò che i Romani non riuscivano a comprendere [sotto tale aspetto la monumentale Storia naturale di Plinio è un disastro].

Il raccontino di Vitruvio sulla corona aurea di Gerone è molto impreciso e fantasioso, sebbene confermato da Proclo nel VI secolo d.C.

La legge dei galleggianti è concettualmente più complessa. Ma se le antiche civiltà marinare costruivano delle navi capaci di navigare in alto mare, ad esempio tra l’isola di Creta e l’Egitto faraonico, ciò significa che le tecniche di navigazione erano già molto evolute. Il che imponeva, tra l’altro, la perfetta conoscenza del cielo, della direzione dei venti e delle correnti marine.

La civiltà antica, certamente diversa – nelle sue forme vitali – da quella che sarà la rivoluzione scientifica moderna, si giovava tuttavia di ritrovati e di scoperte, in un certo senso ‘moderni’. Così va colto il rapporto tra antico e moderno, senza togliere nulla agli antichi e ugualmente alla modernità. [L’enigmatico “disco di Festo”, ritrovato a Creta e non ancora decifrato nella sua scrittura atipica, potrebbe essere addirittura uno strumento analogico per la navigazione, una sorta di mappa celeste che veniva maneggiata dai marinai in una certa maniera, tenendola tra la mano e l’avambraccio].

‘Antico’, in questo senso, è diverso da ‘moderno’. Tuttavia nulla toglie che la vera storia del telescopio, o meglio del cannocchiale a lenti, possa essere molto più antica di quanto si pensi.

L’assiriologo Giovanni Pettinato ha affermato che gli antichi astronomi caldei conoscevano la lavorazione di lenti ottiche in cristallo di rocca. Nelle Rane di Aristofane leggiamo che le donne ateniesi usavano una lente per accendere il fuoco. E’ poi da credere che Leonardo da Vinci, avidissimo ricercatore delle opere di Archimede, fosse un collezionista di fogli antichi, che circolavano in quel periodo, e che contenevano illustrazioni di macchinari ecc., a corredo di opere scientifiche pressoché sparite, o sparpagliatesi in pezzi, con la rovinosa conquista turca di Bisanzio, nel 1453.

Si spiegherebbe così l’insaziabile interesse di Leonardo verso i suoi ritrovati tecnici e i suoi marchingegni che erano, invece, degli studi e dei rifacimenti di quelli contenuti in quei fogli antichi da lui ricopiati e analizzati a prescindere da intenti di realizzazione pratica. I vari codici di Leonardo sono un’opera gigantesca, del tutto impensabile, se non avesse avuto a disposizione dei modelli precedenti e dei materiali antichi da utilizzare. Il solo Codice Atlantico comprende venti volumi in edizione moderna a grande formato. Leonardo tentò anche di costruire un cannocchiale.

Stiamo parlando di una tecnologia apparentemente non applicata, concepita a tavolino e per modelli, sebbene la grande nave di Gerone fosse una realtà ingegneristica di grande spicco insieme a diverse altre meraviglie del passato.

Ci deve essere del vero nella grande fama di cui godè Archimede anche come ingegnere realizzatore di macchine prodigiose e di congegni sorprendenti, se Eutocio di Ascalona, Antemio di Tralles, Isidoro di Mileto ecc., studiarono a fondo le sue opere (Antemio e Isidoro furono gli architetti di Santa Sofia).

3* Tito Livio dà questo ritratto di Archimede: Sommo contemplatore del cielo e degli astri, ma più meraviglioso inventore e fabbricatore di macchine ed ordigni guerreschi, che rendeva vano, con pochissimo sforzo, tutto quello che facevano i nemici con immenso apparato. Ciò che risalta sono le invenzioni. Probabilmente Tito Livio ha inteso associare la sfera celeste e l’Arenario ai ritrovati difensivi durante l’assedio di Siracusa. E’ assai dubbio se tra questi ritrovati figurassero anche gli specchi ustori (noi pensiamo di sì).

L’esempio della grande nave “Siracusa” è poi accostabile a Erone, ritenuto un ingegnere tuttologo, realmente vissuto al principio dell’era volgare, mentre non è impossibile che sotto questo nome si nasconda una scuola o una fondazione alessandrina, specializzata in ingegneria durata nel tempo. In tal caso, Erone, il cui nome in lingua egiziana significa appunto “ingegnere”, non sarebbe altro che l’ultimo esponente di tale scuola, uno che ne raccolse e pubblicò i diversi materiali. [Le opere attribuite a Erone sono disomogenee e di vario argomento ed è assai improbabile che appartengano a un unico autore e che rappresentino un campo di studi originale].

 

I TESTI DI ARCHIMEDE GRANDE GEOMETRA

E GRANDE FISICO DELL’ANTICHITA’

1* Nel 529 d.C. l’imperatore Giustiniano aveva decretato la soppressione ad Atene della storica Accademia di Platone che era continuata con i neoplatonici tra i quali si era distinto Licio Proclo (412 – 485 d.C.).

In Egitto il filone alessandrino era continuato fino a Ipazia, la dotta figlia di Teone, grande seguace del platonismo, che nel 415 fu assassinata per le vie di Alessandria dai cristiani sobillati dal vescovo Cirillo.

L’Egitto, che era entrato a far parte dell’impero d’Oriente, cadde in mano agli Arabi del califfo Omar che nel 641 ordinò la distruzione della Biblioteca che aveva già subito almeno due incendi devastanti, il primo all’epoca di Giulio Cesare e il, secondo all’epoca di Teodosio.

A Costantinopoli, da cui era venuto a dipendere l’Egitto prima della conquista araba, ci furono almeno due riprese nelle scienze: la prima nel sesto secolo, e ancora nel nono. Leone detto “il matematico”, o “il filosofo”, contemporaneo di Fozio, fu il fondatore dell’Università di Costantinopoli nel IX secolo, e fu anche un grande bibliofilo come Fozio.

Diversi epigrammi dell’Antologia Palatina possono essere considerati degli ex libris, o dei colofoni, per i meravigliosi codici in pergamena appartenuti a Leone, e tra questi alcuni preziosi codici archimedei.

L’Antologia palatina attribuisce a Leone l’appellativo di “pagano”, riportando un suo epigramma di tredici esametri (XV, 12), pieno di reminiscenze omeriche dell’Odissea.

Leone, al pari del dotto patriarca Fozio, fu un ricercatore appassionato di codici, particolarmente i codici matematici e filosofici, dei quali certamente curò la trascrizione nella nuova scrittura in corsivo, risuscitando una notevole parte della scienza antica e della filosofia greca, che per lungo tempo erano rimaste neglette, così trasmettendola ai posteri.

Il codice Vaticanus graecus 1594, che contiene un magnifico Tolomeo, reca il marchio di proprietà di Leone. Altri manoscritti più recenti sono a loro volta copie dei codici appartenuti a Leone: così il Laurentianus XXXVII, 4, del XIII secolo, è la copia di un codice di Archimede perduto, poiché alla fine del De quadratura parabolae si legge il nome di Leone con l’appellativo di “geometra”.

Le vicende politiche dell’Impero d’Oriente, sorto nel IV secolo d.C. con Costantino il grande, si trascinarono per oltre un millennio, fino alla drammatica conquista di Costantinopoli nel 1453 da parte dei Turchi.

Abbiamo già detto che sotto il periodo del regno crociato (1204-1261) alcuni scritti di Archimede (il codice A), furono tradotti in latino dal prelato belga Guglielmo di Moerbeke.

Si può ipotizzare che i codici sui quali aveva lavorato nel VI secolo per i suoi commenti Eutocio di Ascalona (una città della Palestina), nell’edizione – come egli dichiara – fattane da Isidoro di Mileto (posteriormente alla soppressione dell’Accademia da parte di Giustiniano), siano stati riversati nella nuova scrittura corsiva e in nuovi codici proprio nel nono secolo da Leone.

L’interesse per Archimede, già rifiorito sotto Giustiniano, all’epoca in cui fu eretta la grande basilica di Santa Sofia, non si era ancora spento.

La preservazione, quantomeno, delle opere principali di Archimede, è dovuta a queste circostanze. Tale continuità include che i papiri di Archimede, che dovevano essere stati conservati ad Alessandria, siano stati per così dire preservati nell’ambito della scuola ellenistica, fino a Erone e a Pappo, ed ancora oltre, per essere poi trasferiti a Costantinopoli e qui trasformati in codici pergamenacei, se già non lo erano in precedenza. All’epoca di Teone e di sua figlia Ipazia, i testi di Archimede dovevano essere ancora accessibili ad Alessandria. Il cristianesimo si occupava d’altro, il mondo dei dotti, che era molto lontano dai problemi attuali della società, sopravviveva a se stesso, nella custodia in chiave puramente dottrinale. Da secoli la società si era allontanata dal sapere e viceversa (un guasto che può sempre tornare ad accadere, se la scienza si allontana dalla realtà e il mondo reale dalla scienza).

Claudio Tolomeo conosceva Archimede. Il patrimonio librario dell’antichità, che era certamente diffuso in oriente come in occidente, ma che alla fine era in buona parte confluito nella capitale dell’Impero bizantino, venne però in larga parte perduto, per una serie di varie circostanze, nelle quali rientravano il cambiamento del gusto e della società, insieme con altri fattori tra cui quello religioso (un monaco palestinese del XIII secolo aveva riutilizzato il codice C di Archimede per un libro di preghiere, cancellando la pergamena e ricucendola in altra maniera). La devastazione del patrimonio librario antico fu di ampia portata, sebbene si siano salvate anche opere minori o addirittura dimenticate e non più lette.

In ogni caso l’Egitto è stato il grande magazzino librario dell’antichità classica. Come risulta dalla testimonianza di Fozio, molte opere non erano più lette nel IX secolo, e da quest’oblio, che era anche fisico, tentò di salvare qualcosa il patriarca, coi suoi riassunti ad uso del fratello.

La conquista crociata del regno di Costantinopoli molto probabilmente comportò altre distruzioni o dispersioni, ma fece anche confluire alcune opere di Archimede nella biblioteca di Federico II, oltre che favorirne la traduzione in latino, alla Corte papale di Viterbo. La conquista turca del 1453 provocò sicuramente la distruzione quasi totale delle biblioteche pubbliche e la dispersione residuale di quanto restava ancora in mano ai privati.

A Costantinopoli furono distrutti dai Turchi codici preziosi e nella devastazione della città si scompaginarono quasi tutte le opere scientifiche che nei secoli erano state trasferite su pergamena. Molti di questi fogli, illustrati da disegni non più comprensibili oppure considerati ormai inutili, finirono per sparpagliarsi in mille modi. Ancor prima del crollo dell’Impero bizantino, in particolar modo sotto il regno crociato, durato circa un sessantennio, la pregiata pergamena di diversi codici era stata riutilizzata per libri sovrascritti.

2* E’ il caso del codice C, scoperto da Heiberg, che conteneva, accanto a tre opere di Archimede, anche alcuni discorsi di Iperide (389-322 a.C.), un antico oratore greco ritenuto secondo soltanto a Demostene, di cui nel 1847 alcuni papiri egiziani avevano già restituito parti notevili di almeno cinque orazioni.

Fozio, nel nono secolo, leggeva ancora Iperide, mentre il lessico di Suda, un’enciclopedia bizantina del X secolo, ci ha tramandato notizie su di lui.

Come poteva essere accaduto che certi fogli del palinsesto archimedeo (fogli 135-138, fogli 136-137, e fogli 174-175) contenessero anche frammenti di Iperide?

E’ probabile che la trascrizione su pergamena riguardasse i testi migliori dell’antichità, quelli che poi ci sono giunti, non importa se in modo parziale.

E’ ovvio che i testi più diffusi, e più accreditati tra il pubblico di lettori, abbiano avuto miglior sorte. Tuttavia Epicuro non si è salvato, se non a Ercolano, però carbonizzato nei raccoglitori di rotoli, dove i manoscritti venivano immessi per evitare l’attacco dei topi e l’umidità. [Sul libro antico e le antiche biblioteche, cfr. Horst Blanck, Il libro nel mondo antico, ediz. Dedalo, 1992, con prefazione di L. Canfora, e Libri, editori e pubblico nel mondo antico, a cura di G. Cavallo, Laterza, III, 2002].

Furono poi gli amanuensi benedettini a trasmettere alla posterità i maggiori testi dell’antichità, almeno quelli diffusi in Occidente, ancora accessibili alla loro comprensione. Nel medioevo furono miracolosamente preservati alcune opere di Archimede a buon frutto per il futuro.

L’Archimede che ci rimane è però una parte alquanto ridotta dell’opera omnia del Siracusano nell’arco di una lunga vita. Le opere rimaste si collocano tutte nella seconda parte della sua vita, quella che si dovrebbe immaginare a meno produttiva, almeno per un matematico.

Archimede potrebbe aver scritto molte altre opere, ancor più interessanti, che probabilmente non furono ben comprese e che dunque rimasero in ombra. Si faranno in futuro altre fortunate scoperte? Di sicuro, saranno altri libri di preghiere. Ciò che si è potuto preservare di Archimede è quanto fu da lui inviato ad Alessandria per Conone, Dositeo ed Eratostene. E dobbiamo ritenere che all’epoca Archimede avesse superato la trentina. Quale immensa perdita!

E’ sorprendente che non ci sia rimasto alcun trattato sulla costruzione di planetari, mentre rimangono alcuni esemplari di questi meccanismi, assai rovinati dagli accidenti subiti. Altre opere antiche ci sono state tramandate nella versione araba, segno evidente del fatto che gli arabi risparmiarono ciò che a loro poteva interessare. Ciò che è rimasto testimonia anche la vita di un grande pensatore e di un uomo di vera scienza. Ed è già un motivo di consolazione la memoria tangibile di un grande spirito.

Forse Archimede morì in un altro modo da come raccontato da Tito Livio e da Valerio Massimo. Forse fu ucciso per ritorsione dagli stessi Romani che ne avevano subìto i guasti. Con la morte stessa di Archimede sarebbero andati perciò perduti molti altri suoi lavori, se è vera la leggenda che i Romani avrebbero bruciato 15 ceste di manoscritti ovvero suoi volumi. Opere perdute di Archimede furono sicuramente il trattato sui numeri inviato a Zeusippo, il De viatico (cioè “sul modo di viaggiare”, uno studio probabilmente vertente sul problema della longitudine), il De libris accennato da Pappo, e il trattato sulla costruzione della sfera celeste riportato da Carpo.

Il Metodo meccanico, insieme a qualche foglio dello Stomachion, riapparve invece nel 1906 dal palinsesto utilizzato per un libro di preghiere, mentre il terribile problema bovino era stato scovato nel XVIII secolo, in un fondo di biblioteca.

LA MISURAZIONE DELLA TERRA

1* Nelle sue opere Archimede si esprimeva sempre in modo impeccabile, come farebbe un matematico moderno. Era un individuo orgoglioso, sincero, ironico, e sicuramente giocò qualche brutto scherzo ai presuntuosi suoi contemporanei, inviando loro false dimostrazioni per vedere come reagivano.

Probabilmente c’era stato qualcuno che si faceva bello con i suoi teoremi, né si può escludere che a un certo punto Archimede sia entrato in urto, per seri motivi, con Eratostene, il dotto alessandrino che era divenuto Bibliotecario, e che si piccava d’essere un grande matematico oltre che un illustre filologo, un bravo geografo e uno studioso di Platone.

Eratostene aveva misurato il valore del raggio terrestre. Le sue misure non erano così esatte come pretendeva, perché gli errori sistematici si erano compensati tra loro. Il metodo usato per tale misurazione non era neppure il più appropriato, e non era nemmeno originale, poiché si deve presupporre che gli antichi Egiziani avessero già compiuto o almeno concepito in qualche modo tale impresa, approfittando della posizione geografica dell’antica città di Syene posta all’incirca sul tropico.

Gli antichi Egiziani sapevano che la Terra è una sfera e conoscevano almeno empiricamente il calcolo del cerchio per stabilire anche il valore angolare del grado di meridiano? A queste domande si può rispondere che sebbene la misura del cerchio fosse dovuta ad Archimede, essi erano comunque a conoscenza del valore empirico, sufficientemente utile e preciso, del rapporto fisso tra il diametro del cerchio e la circonferenza, facilmente ottenibile in concreto con una semplice cordicella che avesse circondato un fusto rotondo ad esempio una colonna. Quel rapporto era invariante per ogni cerchio. Perciò gli antichi Egiziani erano in grado di misurare la circonferenza e quindi anche il raggio terrestre calcolando la proporzione angolare dell’inclinazione del sole alla stessa ora, al momento di culminazione superiore da due luoghi abbastanza lontani ma allineati, di cui fosse già nota la distanza in passi, appunto misurata da “mensori” pedestri o “camminatori”.

Perché a Syene, nell’alto Egitto, esisteva già un antico pozzo, in cui il sole a mezzogiorno del solstizio d’estate, si rifletteva a piombo? Perché era noto che a quella latitudine il sole quel giorno si trovava sulla verticale. Cosa che non avveniva nelle città e nei templi del basso Egitto. Pertanto la terra era rotonda. Aveva la forma di una sfera. Per calcolarne la grandezza occorreva soltanto trovare due luoghi lontani, uno di essi era Syene, allineati sullo stesso meridiano. La civiltà egiziana che venerava il sole e conosceva il calcolo del tempo e le meridiane, era sicuramente in grado di concepire l’impresa della misurazione della grandezza della Terra mille anni prima di Eratostene. Una stella riconoscibile in cielo che a mezzanotte esatta culminasse sulla verticale dell’osservatore, indubbiamente avrebbe avuto il medesimo percorso su tutti i luoghi allineati tra loro. Quella medesima stella osservata da Syene sarebbe stata riconoscibile, anche se non gettava alcuna ombra. Al posto della stella andava poi messo il sole alla data del solstizio estivo. Il sole gettava la sua ombra con lo gnomone. Intanto si sapeva già che i due luoghi erano allineati sul meridiano. Non rimaneva che calcolare con estrema pazienza le distanze pedestri tra i due luoghi che si sapevano già essere allineati tra loro anche se molto distanti. Il procedere sempre diritto dei misuratori di passi consisteva nel prolungamento continuo della medesima linea iniziale, già individuata, che all’inizio doveva essere lunga alcuni chilometri. E’ impossibile ritenere che ciò non fosse alla portata dei costruttori delle piramidi tanto più che questi straordinari monumenti erano collegati al cielo stellato. I sacerdoti Egiziani avevano conservato i documenti o le conoscenze di quest’antica impresa della misurazione della Terra, Eratostene ne venne a conoscenza. Insomma, i matematici di Alessandria perfezionarono il metodo antico e/o rifecero i calcoli, ma non spetterebbe a loro il merito concettuale della grande impresa della misurazione della Terra.

A che serviva conoscere con una certa precisione il valore del raggio terrestre e l’ampiezza approssimativa del grado di meridiano, se non per stimare le distanze geografiche e per la navigazione in alto mare? Nasceva la geografia scientifica, ma ciò non toglie che la conoscenza della grandezza della Terra rimanesse un dato sacrale, insieme allo studio del cosmo. Ciò doveva far parte dei segreti delle Piramidi, vecchie di millenni rispetto ai Greci.

2* Il metodo impiegato da Eratostene per misurare la circonferenza della Terra non doveva essere originale, ma era più accurato nelle operazioni di stima. L’angolo di conferenza corrispondeva all’inclinazione dei raggi solari. Conoscendo il valore approssimato della base, la distanza tra Alessandria e Syene, si poteva conoscere il valore della circonferenza terrestre con buona approssimazione. La procedura richiedeva concettualmente la comprensione della sfericità terrestre, che però non poteva essere sfuggita ai costruttori delle piramidi, se avessero usato il minimo raziocinio scientifico.

Rotondi e solidi erano la luna e il sole raggiante (osservabile con un vetro affumicato). Le vele delle navi che arrivavano in porto salivano lentamente dall’orizzonte. La tessa cosa quando se ne allontanavano. Da una montagna si ampliava la vista del territorio circostante. L’orizzonte marino era curvo.

Le conoscenze dei greci, riportate da Aristotele, non erano originali rispetto a quelle più antiche. La sfericità della terra non era una scoperta greca, e la geometria era già sorta in Egitto, quando Talete l’apprendeva dai sacerdoti. Quei sacerdoti egiziani che rimproveravano ai Greci la loro fanciullezza (adesso si capisce per quale ragione), ma che si complimentarono per l’acume di Talete nello stabilire in questo modo l’altezza delle piramidi [spesso i racconti di questo genere si riferiscono a un retroscena più complesso, anche se dalla narrazione semplicistica ciò non appare].

La civiltà umana è molto più antica di quanto si pensi e questo fatto torna perfettamente naturale. Fu l’invenzione della scrittura a far decollare le antiche civiltà. Da una base minima di solide conoscenze, si può stimare a non più di cinque secoli il periodo d’evoluzione per una vera civiltà organizzata. Quindi non più di 20 generazioni, tante quante le generazioni del frammento 108 di Empedocle a proposito della sapienza del veggente, ma a condizione d’una effettiva continuità.

Possiamo immaginare ciò che probabilmente accadde. Eratostene, divenuto il nuovo Bibliotecario, aveva ritrovato un antico papiro sacro, in cui in cui era descritta la procedura di misurazione della circonferenza della Terra. Egli volle dunque verificare quelle stime, con nuove misurazioni, anche perché la casa regnante era interessata a imprese geografiche e ai traffici commerciali.

Piazzi Smith, astronomo reale scozzese, non era un folle ‘piramidologo’ come si ritiene comunemente. In qualche cosa aveva ragione. Le piramidi non sono il monumento della follia del faraone, come sosteneva Erodoto, ma qualcosa di più enigmatico e misterioso.

Quando Talete calcolò dall’ombra gettata da uno gnomone (lunga quanto il bastone stesso) l’altezza corrispondente dell’ombra della grande piramide di Cheope, quel suo atto d’intelligenza conteneva in sé un secondo significato: l’ombra dello gnomone era serviva anche a stimare la grandezza della Terra. A maggior ragione i sacerdoti egiziani ne rimasero colpiti giacché sapevano che dall’inclinazione del sole in due luoghi diversi e allineati sul meridiano erano state calcolate a una certa data le dimensioni del globo.

La piramide di Cheope ha base quadrata con gli angoli orientati sui quattro punti cardinali. La sua altezza è inferiore alla base. Il significato astronomico della grande piramide è chiaro. Diogene Laerzio (III d.C.), avendolo ripreso da Ieronimo, affermava che Talete misurò le piramidi basandosi sulla loro ombra, dopo aver osservato in qualemomento la nostra ombra è uguale alla nostra altezza. Quest’aneddoto, che tra l’altro nasconde le vere origini della geometria greca, è anche irrazionale. La piramide nascondeva la propria altezza, ma anche la base: con ciò anche una parte dell’ombra che servirebbe a Talete (cfr. R. Casati, La scoperta dell’ombra, Rizzoli 2000, pag. 99). Diogene si riferiva alle piramidi, e non a una piramide in particolare (ma la piramide per eccellenza, era quella di Cheope). Insomma Talete doveva conoscere il valore della base (cioè la metà della base della piramide), e poi aggiungervi la sporgenza dell’ombra oltre la base. Non era un granché. Il paradosso è che ciò che si doveva sapere per misurare l’altezza della piramide, ricorrendo al metodo dell’ombra, basta anche per misurarla, senza ricorrere a questo metodo. Talete precedeva Pitagora di almeno una generazione. Dobbiamo concludere nel senso che l’aneddoto su Talete e le piramidi, riportato da Diogene Laerzio, contiene un’allusione oscura alla antica misurazione della terra, col metodo egiziano dell’ombra dello gnomone. Quando il sole è a 45 gradi nel cielo, il pezzo di ombra che sporge alla base della piramide non serve a molto di per sé: si deve ancora calcolare la lunghezza della parte nascosta dell’ombra. Tuttavia l’ombra poteva suggerire la figura proiettata e anche l’idea della geometria piana e di quella solida. Mentre l’orizzonte marino è come un cerchio.

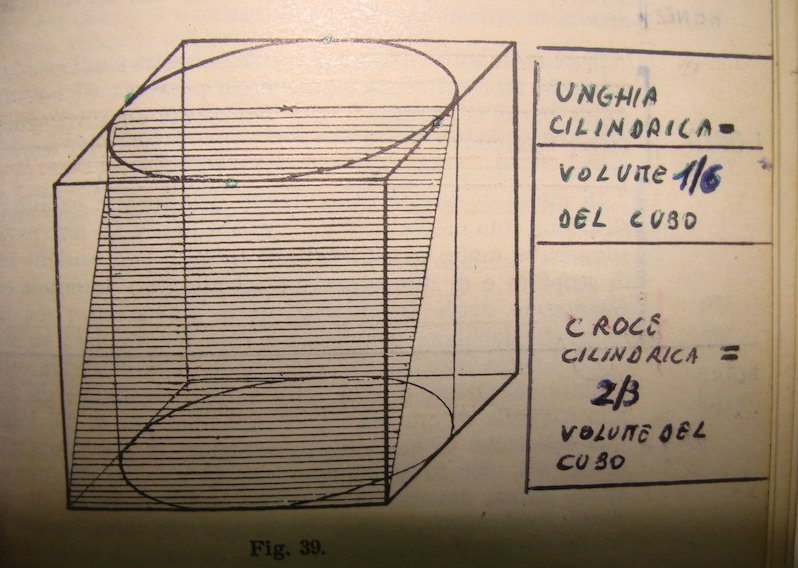
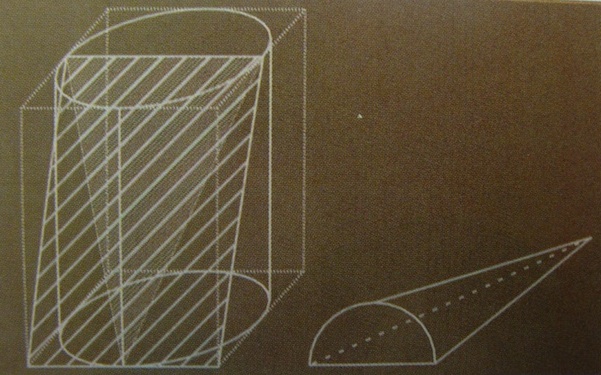
3* “Geometria”, in lingua greca, significa “misurazione della terra” (termine appropriato per intendere anche qualcosa di più che non la semplice misurazione dei nuovi confini dei campi, dopo le periodiche alluvioni del Nilo). I Greci prima di Archimede non erano ancora venuti a capo dei misteri della geometria curva (che richiede infatti l’impiego del calcolo infinitesimale per la misurazione di tutte le aree curvilinee), malgrado le lunule di Ippocrate di Chio, alle quali si avvicinano l’arbelon e il salinon di Archimede nel libro dei Lemmi. Ma, i Greci, a questa geometria curvilinea si erano comunque interessati: non fosse altro che per ragioni pratiche, almeno per quanto concerneva certi solidi regolari come il cono, la sfera e il cilindro (oggetti archimedei per eccellenza). La duplicazione del cubo era un tipico esempio di problema sacro, strettamente collegato agli altari. Si trattava di un problema numerico, quello della radice cubica. E’ invece facile vedere che duplicando il lato del cubo, il suo volume quadruplica. La stessa cosa avviene per una superficie quadrata. Ciò significa che ci troviamo davanti ad un “invariante” nel passaggio dalla seconda alla terza dimensione, e i geometri greci ne avevano cognizione, a cominciare dal “punto senza dimensione”, introdotto da Platone anche perché il cono e la piramide terminano in un punto ideale, che non può non esistere concettualmente parlando.

Gli indivisibili del quadrato, chiamiamoli così, sono in analoga corrispondenza agli indivisibili del cubo, secondo un principio di continuità dimensionale.

Il piano del quadrato è idealmente composto di un’infinità di segmenti identici, e così il cubo, senza alcuna variante, da un’infinità di quadrati privi di spessore.

I pitagorici erano stati i primi a introdurre le sezioni coniche, servendosi di un cono retto, iscrivibile in un cubo. Conoscevano il cerchio, l’ellisse, la parabola e l’iperbole almeno come linee curve, anche se ignoravano a quel tempo certe altre proprietà geometriche che vennero approfondite in età alessandrina ad esempio da Apollonio di Pergamo.

Empiricamente, gli atomisti ionici conoscevano già il volume relativo della piramide retta, rispetto al cubo, e il volume del cono retto rispetto al cilindro retto. Il rapporto costante di 1/3, valido nei due casi, costituisce un invariante. Tale conoscenza veniva da prove empiriche, concepite riempiendo di sabbia oppure d’acqua dei recipienti di quella data forma.

La ‘quantizzazione’ di tipo ‘granulare’ del volume era un espediente ideale. In modo geometricamente coerente, riducendo all’infinito la piccolezza del punto, come un granello infinitamente piccolo di sabbia, fino al suo totale annichilimento, come aveva già detto Platone si otteneva un nuovo ente geometrico di dimensione nulla.

In questo senso, il punto ‘zero’ era il culmine estremo di un cono o di una piramide ideale o il punto di centro in cui un cerchio si annullava.

Da questa idea, astratta ma funzionale, si poteva passare alla considerazione progressiva delle altre 3 dimensioni vicine ai sensi. L’ombra di un corpo ha chiaramente dimensione 2, se il corpo stesso ha dimensione 3 (cioè altezza, larghezza e spessore).

Il segmento, o linea ideale, aveva dimensione 1, essendo priva di spessore e di larghezza). L’area delimitata da un perimetro era di dimensione 2, ma infinitamente sottile. I corpi solidi ideali, come il cubo, la sfera, la piramide, il cono e il cilindro, erano di dimensione 3. Questi concetti appartenevano sia alla geometria pitagorica, che a quella platonica.

Platone, e pitagorici prima di lui, aveva integrato la concezione, granulare e numerica degli atomisti ionici, col continuo geometrico. Una linea, comunque estesa, che rimanesse tuttavia un segmento, conteneva già un’infinità di punti, perché idealmente poteva essere spezzata infinite volte. Esisteva anche una gerarchia di ‘infiniti’. La linea retta infinita che dimensione avrebbe? La curva di Peano indicherà che appartiene alla dimensione 2, identica per esempio a quella del quadrato.

La definizione moderna di dimensione è diversa, ed è differente anche la definizione moderna di punto. Questo non ci interessa, poiché Platone aveva già definito il punto come ente geometrico senza dimensioni.

Lasciamo da parte la questione del numero zero: ignoto ai greci e introdotto si dice dagli Arabi, quando nell’Odissea, canto di Polifemo, dovremmo cogliere un’allegoria dello zero-nessuno e del mistero dei numeri primi (il numero dei compagni di Ulisse e il numero delle pecore del gigante con un solo occhio, accecato con un palo rovente, era un numero primo: 13 in tutto, con Ulisse, marinai e pecore). Tu chiedi il nome glorioso, o Ciclope; io te lo dirò, ma tu dammi il dono che mi hai promesso. Nessuno è il mio nome, Nessuno mi chiamano padre e madre e tutti gli altri compagni. [R. Kalan, Zero, Rizzoli 1999, capitolo Per i grecinon aveva nome].

4* La geometria delle figure piane e dei corpi ideali conteneva in sé i paradossi dell’infinito. I numeri naturali di Pitagora erano infiniti come i loro quadrati. Era poi evidente che un bel cubo di marmo pario, di lato doppio rispetto al cubo unitario di riferimento, pesava 4 volte il cubo dello stesso marmo di lato unitario. Il gioco dei cubetti per i bambini è antichissimo e in qualche modo risponde alla teoria della reminiscenza esemplificata da Socrate nel Menone con la duplicazione del quadrato fatta eseguire a uno schiavetto non scolarizzato. Il ‘grande’ e il ‘piccolo’ non interessavano ai geometri greci, ma le forme. In questo senso la sfera era la più ideale e la più perfetta di tutte le altre forme solide. Si comprendeva già, intuitivamente, che a parità di superficie la sfera racchiudeva il massimo volume possibile. Mentre il cubo era perfettamente squadrato, e perciò facile da calcolare numericamente, così però non era per la sfera, la cui assoluta levigatezza e totale rotondità la rendevano un oggetto ‘difficile’, sebbene assolutamente bello e affascinante: il Cosmo intero doveva avere la medesima forma di una Sfera. Sferici erano la luna e il sole.

La sezione di un cubo è sempre un quadrato. Quella di una sfera è un cerchio decrescente, fino a ridursi a un punto infinitesimo, nelle 4 direzioni possibili. Anche nel cono, nella sfera e nella piramide, il punto senza dimensioni di Platone aveva il suo significato di limite. Ugualmente, un cerchio, ad esempio un circolo creato nell’acqua, si poteva allargare all’infinito oppure annullare restringendosi in un solo punto, fino a sparire nella calma piatta.

Qual era il possibile rapporto tra il cerchio e il quadrato circoscritto, tra il cubo contenente e la sfera ivi perfettamente contenuta, tra il cubo e la piramide, tra il cono, la sfera e il cilindro? E quale il rapporto tra la circonferenza e il diametro del cerchio, se il rapporto tra il lato del quadrato unitario e la sua diagonale era un numero irrazionale, espresso dalla radice quadrata di due?

Tali ‘domande’ si erano già affacciate all’attenzione dei geometri greci, anche se mancavano ancora le risposte.

La dicotomia pitagorica tra ‘retto’ e ‘curvo’ attendeva dunque un grande maestro digeometria, auspicato da Socrate nella Repubblica, che indagasse a fondo su tali rapporti. Questo maestro sarà Archimede. Intanto abbiamo ritrovato il titolo di alcune sue opere fondamentali, e persino la sfera e il cono, che ornavano emblematicamente la sua tomba ritrovata a Siracusa, nascosta tra i rovi, da Cicerone.

5* Il cono retto, ma anche ogni altro cono, poteva essere tagliato da un piano, generando 4 sezioni coniche differenti: la parabola, l’iperbole, l’ellisse e il cerchio dotati di certe specifiche proprietà geometriche. Il sogno fatto da Cartesio diventerà la geometria analitica piana delle sezioni coniche. Gli assi cartesiani presuppongono il piano infinito ripartito in quadranti. Geometria e numero si fonderanno. Molte equazioni riceveranno una rappresentazione cartesiana.

L’attenzione dei pitagorici si era orientata non solo verso il numero, ma anche nei riguardi dello spazio geometrico, con la geometria che era nata nell’antico Egitto per esigenze pratiche di misurazione dei campi dopo le piene periodiche del Nilo [ma abbiamo già supposto che gli antichi Egizi avessero saputo misurare la circonferenza della Terra molti secoli prima di Eratostene]. A nostro avviso è stata però l’ombra a generare la geometria e le luci del cielo notturno a elevarla così in alto, tanto che anche Newton, che aveva già inventato il calcolo infinitesimale, tuttavia non volle rinunciarvi nella sua rappresentazione del Cosmo e delle orbite gravitazionali, mentre Keplero si era servito dei 5 solidi platonici nel Mistero Cosmografico pubblicato nel 1596.

L’ellisse aveva un carattere sacro: ellittici erano gli antichi castellieri umbri, ellittica era la forma dell’anfiteatro romano, ellittiche le prime mura di Pompei, il cui nome evocatore (Pompe, come ricorda Marziano Capella) sembrava associato alle mitiche imprese di Ercole (ma pompe era anche il nome etrusco del numero 5).

Con lo studio delle sezioni coniche, portato a perfezione geometrica da Apollonio di Pergamo in età alessandrina, la geometria greca aveva predisposto quanto sarebbe poi occorso a Keplero per formulare le sue tre leggi orbitali e a Cartesio per introdurre la geometria analitica con equazioni di primo grado e poi di grado superiore. Il ‘numero’ e le ‘forme geometriche’ sembravano corrispondersi. L’esposizione della dinamica celeste di Newton avvenne, nei Principia, ricorrendo soltanto a rappresentazioni geometriche. [Richard Feynman nel 1964 scoprì un’altra dimostrazione geometrica dei moti planetari rispetto a quella fornita di Newton].

La terza legge orbitale di Keplero, che riassumeva in sé le precedenti e che permise a Newton di stabilire la meccanica celeste correlata all’azione della forza di gravità, di cui ancora s’ignorava il valore essendo nota soltanto la sua accelerazione, correlava a una costante il rapporto tra il quadrato dei tempi orbitali e il cubo del semiasse maggiore dell’orbita ellittica per ciascun pianeta.

Tempo e spazio rappresentano il movimento. I pianeti orbitano intorno al sole secondo una ‘legge’ che soltanto la teoria generale della relatività di Einstein chiarirà tre secoli dopo Newton, che però non aveva finto ipotesi.

La terza legge orbitale di Keplero, a prescindere dalle cause del movimento di rivoluzione ellittica dei pianeti intorno al sole centrale, risponde nella sua essenza a una relazione di tipo ‘dimensionale’.

Se consideriamo un’orbita planetaria come “perimetro”, cioè alla stregua di una linea svolta di dimensione 1, allora l’area ellittica battuta dal vettore (o semiasse maggiore) dell’orbita di un pianeta, ha valore dimensionale 2.

Scalando di una unità, dal “quadrato” dei tempi al “cubo” dello spazio, analogamente a quanto aveva fatto Platone nel mito della caverna, otteniamo un invariante, la costante di Keplero. La terza legge orbitale è pertanto un ottimo esempio d’invariante, scalando di una dimensione e traducendo un fenomeno dinamico, dovuto alla ‘forza di gravità’, in due fatti geometrici distinti ma correlabili. Spazio e tempo si corrispondono nelle orbite planetarie in base a un rapporto costante, la cui giustificazione dipende – in re ipsa – dalla natura dimensionale della rivoluzione intorno al sole, capace unificare fatti apparentemente diversi, ma composto dal medesimo evento.

Tutto ciò ne rappresenta l’essenza immutabile di una “necessità” o Ananke puramente geometrica, di tipo platonico-parmenideo.

Strano ma vero: e a prescindere dalla natura della forza di gravità, poiché c’è perfetta corrispondenza tra l’area battuta dal vettore e il perimetro dell’orbita, e tra il tempo e la distanza dell’ampiezza orbitale.

Quest’analogia è ricca di significato poiché iva corrisponde a un’essenza necessaria.

Abbiamo trasformato il rapporto costante di Keplero tra il quadrato dei tempi di rivoluzione (un perimetro) e il cubo della distanza del semiasse maggiore (un’area), nell’invariante x/x = 1, che rappresenta l’intima unità dinamica del fenomeno, giacché si è potuto stabilire per lo stesso fenomeno, la relazione geometrica dimensionale tra spazio-perimetro e tempo-area, rispettandone i loro valori. Il “perimetro” ellittico di un pianeta in rivoluzione intorno al sole centrale e la traiettoria orbitale correlata hanno valore dimensionale identico, pari a 1. Se ci riferiamo alle “aree”, di dimensione 2, dovremo necessariamente utilizzare il “quadrato” del tempo per rendere omogeneo il sistema dinamico in sé e per sé. In termini di “area” i tempi sono necessariamente dei quadrati, hanno cioè dimensione 2.

La terza legge orbitale di Keplero ha questa espressione: il valore al quadrato del periodo orbitale (tempo t) di un pianeta sta al valore del cubo del semiasse concernente la relativa orbita ellittica, secondo un rapporto costante, valido per tutti i pianeti. Se scaliamo di un fattore 1 la relazione ‘quadrato dei tempi’ e ‘cubo delle distanze’, ritroviamo sempre la figura geometrica di un’orbita ellittica (invariante topologico), vista secondo il modello a dimensione 1 del perimetro orbitale e il modello a dimensione 2 dell’area spazzata dal semiasse. Non potendo mutare l’invariante topologico dell’ellisse, che caratterizza le orbite planetarie, il fattore di correlazione dimensionale rappresenta anche una costante dinamica. Insomma il moto orbitale dei pianeti corrisponde alla scala gerarchica delle dimensioni di corpi solidi.

Il cubo delle distanze orbitali, o semiasse, è il fattore ‘dimensionale’ 3, tipico dei corpi solidi nello spazio tridimensionale, che a sua volta implica il fattore dimensionale 2 dei tempi di rivoluzione intorno al sole, tipico delle aree. Scalando di un’unità, è lo stesso identico rapporto. Il perimetro o segmento srotolato dell’ellisse orbitale (dimensione 1) corrisponde, in senso dinamico, all’area stessa dell’orbita (dimensione 2). Il tempo o perimetro srotolato dell’ellisse deve elevarsi al quadrato per raggiungere omogeneamente il valore cubico del semiasse orbitale, che nella medesima rivoluzione del corpo solido intorno al sole è rappresentato da un’area. La costante di Keplero (terza legge orbitale) si fondava su invarianti dimensionali caratterizzanti qualsiasi orbita chiusa di rivoluzione intorno al sole centrale. L’orbita ellittica dei pianeti intorno al sole comportava la percorrenza di aree uguali in tempi uguali (seconda legge di Keplero). Quest’uguaglianza tra tempi e aree inerisce alla inseparabilità (o invariante) tra l’arco di dimensione 1, riportato al perimetro orbitale, e l’area di dimensione 2 riportata alla superficie complessiva sottesa da quell’arco ellittico, fino al fuoco dell’ellisse dato dalla posizione centrale del sole rispetto all’orbita planetaria. Le tre leggi orbitali di Keplero erano di tipo osservativo, ma l’essenza di queste leggi è di tipo geometrico. Il fenomeno ‘dinamico’ è apparente. Non esiste alcuna forza di attrazione tra i corpi celesti, ma agiscono invarianti geometrici come Ananke, quale necessità.

Avrà attraversato la mente di Archimede il problema in sé della “gravità”, poiché si occupò anche dei centri di gravità nei corpi? I proiettili scagliati dalle sue catapulte compivano visibilmente delle traiettorie paraboliche, come qualsiasi arciere sapeva dovendo mirare un po’ al disopra di un bersaglio lontano, per poterlo colpire. La tendenza dei corpi a cadere in basso, sulla verticale (a parte il problema del moto parabolico composto), da che cosa poteva dipendere? L’azione a distanza, senza alcun contatto fisico, era assai misteriosa, sebbene costantemente esibita dalla natura. Se Aristarco, la cui opera era ben nota ad Archimede, aveva ipotizzato il sole al centro dell’universo (mentre i pitagorici professavano una dottrina affine), quale forza condizionava le orbite planetarie a continuare per sempre nel loro giro regolare (grande anno)? Il grande Siracusano ci avrà riflettuto. Tanto più che aveva costruito modelli di sfere celesti e/o di planetari meccanici. Poteva la geometria risolvere il problema della gravità, non solo dei centri di gravità dei corpi, che Archimede risolse brillantemente? Archimede avrà tentato di reperire un invariante concettuale per la gravità, magari collegandolo alle leggi del galleggiamento. Una palla di ferro piena, lasciata cadere in acqua, cadeva più rapidamente di una palla di ferro con un vuoto interno. Ma eliminata ogni resistenza, quale sarebbe stato l’invariante necessario, l’Ananke per la caduta dei gravi nel vuoto? C’è da scommettere che Archimede avesse capito che nel vuoto i corpi cadono alla stessa ‘velocità’, a prescindere dal loro peso (l’estrapolazione era elementare, anche se la pseudo fisica di Aristotele lo negava). Ma la gravità in sé, era faccenda ben più difficile. Che cosa sosteneva la Luna, relativamente vicina, il cui moto orbitale intorno alla Terra era evidente? Quant’era grande e potente il Sole per illuminare la Terra e la Luna?

L’invariante che Archimede poteva mettere in conto era che la Luna non cadeva sulla Terra perché nemmeno se ne allontanava troppo (Archimede sapeva che la grandezza angolare della luna variava periodicamente nel tempo se pur di pochissimo).

Crediamo che questi pensieri abbiamo attraversato la sua mente e poi che la risposta che si poté dare fu questa: su grande scala la gravità è una forma di equilibrio tra una condizione e l’altra, su scala ridotta la gravità attiene al centro della Terra. Il ‘peso’ dei corpi manifesta la gravità, ma il movimento rotatorio la annulla. Nulla di più e nulla di meno anche se non possiamo sapere dalle opere rimasteci se si accostò a questo problema e come eventualmente lo affrontò. Tuttavia, il problema della gravità, almeno come tale, non poteva e non doveva sfuggirgli. Archimede è uno dei giganti sulle cui spalle si arrampicò Newton.

LA GEOMETRIA DELLE FIGURE E DEI CORPI CURVI

1* L’esempio ‘dimensionale’ riferito a Keplero aiuterà a comprendere come Archimede avesse potuto intuire, prima d’ogni dimostrazione vera e propria, i suoi principali risultati nel campo della geometria piana e solida del “curvo”.

Dobbiamo partire dalla rappresentazione simbolica della tetraktys pitagorica che aveva al suo vertice il numero 1, rappresentabile da un punto oppure da una berretta verticale. Dopo le prime 3 file, la tetraktys terminava con 4 numeri: 7, 8, 9 10 (quarta fila). Ognuna delle 4 fila progressive aveva tanti numeri (somma fino a 10), quanto l’ordine numerale della file stessa.

Il numero 10 derivava dalle dieci dita per contare. Il sistema decimale si basa su questo dato fisiologico elementare, mente in sistema sessagesimale era una rappresentazione celeste, connessa alla fascia dello zodiaco (le 12 costellazioni individuate dagli astronomi assiro-babilonesi nell’eclittica) e quindi collegata alla suddivisione in gradi del cerchio (per cui un oggetto celeste sembra spostarsi nel cielo notturno di 15 gradi ogni ora). I monumenti di pensiero della civiltà antica sono il sistema decimale (sebbene con grave limite nella facilità dei calcoli non fosse impiegato lo zero) e il sistema sessagesimale (per questa ragione l’orologio ha 12 ore).

Il dodecaedro era un solido cosmico. Il cerchio si componeva di 12 volte 15 gradi = 360 gradi. La geometria e il numero permettevano l’intelligenza delle cose. Senza di essi non poteva esistere una vera civiltà, non ci sarebbe mai stata una possibilità di sviluppo. Il computo e il riconoscimento delle forme sono la base di ogni civiltà accanto al trasferimento del pensiero nei simboli e nella scrittura.

Il simbolico ma semplicissimo schema o diagramma della tetraktys pitagorica correlava i dieci numeri naturali della decade, come numeri triangolari (1, 3, 6, e 10), allo stesso tempo alludeva alla successione ordinata delle 4 ‘dimensioni’ in geometria: il punto, il segmento, il piano e il volume. Se il numero è potenzialmente infinito, lo è anche lo spazio. La sola maniera per collegare il numero (rappresentato dalla decade) ai semi dello spazio geometrico era il concetto di dimensione. La tetraktys pitagorica, come del resto già indicava questo nome, serviva allo scopo di tenere unite l’aritmetica e la geometria, col numero che era la misura di tutte le cose.

Quando emergerà con Platone il concetto di “punto senza dimensione” (cioè dimensione nulla, anche se i Greci non fecero mai uso dello zero nella loro aritmetica), la ‘quarta dimensione’ sarà con Archimede quella del piano ideale infinito, generatore ideale di tutte le ‘forme’.

In Euclide un punto è ciò che non ha parti, mentre una retta è una linea che giace ugualmente su se stessa con i suoi punti. Queste definizioni venivano da Platone. Ciò che non ha parti non coincide con lo zero. Se consideriamo l’unità come indivisibile (cioè solo come intero), la tetraktys pitagorica rappresenta anche le 4 dimensioni. Il punto in cui terminano e si annullano il vertice di un cono o di una piramide, oppure il centro esatto di un cerchio in cui il circolo stesso si restringerebbe fino ad annullarsi, danno l’idea di punto geometrico. La quarta riga della tetraktys simbolica (numero triangolare 10), rappresenta il piano ideale infinito, mentre di un corpo solido a 3 dimensioni i parametri numerici sono 6, come appunto nel calcolo orbitale moderno dei corpi planetari immersi nello spazio (terza riga della tetraktys).

Il settimo libro della Repubblica di Platone (governata dai sapienti), si apre col mito della caverna, per arrivare alla necessità che il sapiente debba conoscere la matematica, la geometria e l’astronomia. L’opera fu composta tra il 388 e il 367 a.C.

Nel mito, la condizione dei prigionieri all’interno della caverna rappresenta la mera conoscenza delle realtà sensibili, che sono come l’ombra delle cose. La conoscenza vera richiede una ‘dimensione’ in più, la conversione verso la luce e la visione delle realtà intellegibili. Cioè il campo proprio della filosofia, della matematica e della geometria.

2* La superficie sferica è perfettamente curva ed è idealmente composta da infiniti punti senza dimensione, nessuno dei quali è allineato all’altro. Il concetto di superficie sferica è di perfetta bellezza e al tempo stesso delimita il volume della sfera. La superficie della sfera è differente da qualsiasi altra superficie ed è quella capace di racchiudere il massimo volume per unità di superficie. La sfera è il solido di rotazione di un cerchio.

Archimede si interrogò anche su altri solidi di rotazione, i conoidi e gli sferoidi, come volumi prodotti dalla rotazione di ellissi o parabole, e si interessò sul loro volume rispetto a quello analogo del cilindro [Torricelli, allievo di Galileo, si occuperà dell’iperboloide acutissimo, mentre nel 1657 Fermat pubblicò il metodo per la quadratura d’infinite parabole e di infinite iperboli].

Cerchio, ellisse, parabola e iperbole sono sezioni coniche. Emergono dunque il cono, il cilindro, la sfera, i conoidi e gli sferoidi [cioè la nuova geometria di Archimede, che racchiude in se qualcosa di sperimentale e persino di meccanico, ma che rimaneva al tempo stesso, ideale e astratta].

Il grande e il piccolo sono concetti relativi. Ciò che conta è la forma. La forma perfetta è quella della sfera. La sfera, la cui ousia è però diversa da quella del cilindro (che è solido generato dalla rotazione di un quadrato oppure di un rettangolo), sebbene sorprendentemente i rispettivi volumi, quelli della sfera e del cilindro, siano correlabili, come appunto scoprì Archimede, che trovò la meravigliosa relazione ‘pitagorica’ della sequenza discendente di rapporti 3-2-1 rispettivamente per i volumi del cilindro, della sfera e del cono inscritti nel medesimo cubo contenente questi solidi ‘curvi’.

Nel mito della caverna sfugge ai prigionieri il segreto della quarta dimensione che difatti non è rappresentabile attraverso i sensi. Platone semplificava il non rappresentabile dai sensi umani con un’analogia piena di potenza simbolica, scalando di una dimensione (come abbiamo mostrato con riguardo della terza legge orbitale di Keplero).

Servendosi dell’analogia bidimensionale delle ombre proiettate sulla parete della caverna dai corpi eterni illuminati dalla luce, che trascendono i senzienti, Platone ha saputo esprimere un’allegoria affascinante, piena di suggestione (e ne deriverà anche la geometria proiettiva del XVIII secolo: cfr. R. Casati, La scoperta dell’ombra, Mondadori, 2000; R. Rucker, La quarta dimensione, Adelphi, 1994, pp. 23 segg.). L’allegoria della caverna consisteva nell’espediente dell’analogia. Il mistero del Cosmo [per esempio le ombre proiettate dalle eclissi ] è ‘quadridimensionale’ nel senso che in questa ‘analogia’ (termine impiegato da Archimede nell’Arenario) il tessuto di tutto lo spazio puro (nella sua infinita durata) è concepibile alla stregua della buccia o superficie ideale di una sfera, che deve essere di dimensione 4 giacché il volume della sfera – o contenuto del mondo sensibile nel caso del rotondo sfero di Parmenide e di Empedocle – è di dimensione 3. La superficie sferica, che ha sempre il suo valore concreto, determinato dall’ampiezza del raggio, dipende anche dalla costante del cerchio – o “numero trascendente” pigreco – e dal fattore < 4 > che è poi il valore dimensionale del piano infinito.

La sequenza della tetraktys fino alla quarta fila esprimeva simbolicamente il principio della continuità dimensionale, attraverso i 10 numeri della decade e i primi 4 numeri triangolari, fino alla contemplazione “pitagorica” dell’universo sferico. Archetipi di questo genere erano anche le 10 tavole di Mosè e la raffigurazione del mistero divino tramite un triangolo equilatero. L’archetipo cosmico era rappresentato dalla decade pitagorica per mezzo della tetraktys culminante nella quarta dimensione.

A quest’archetipo pitagorico s’ispirarono Parmenide, Empedocle, Platone, e infine Archimede. Lo spazio puro era un piano infinito che poteva generare ogni cosa. Il numero 4 della tetraktys pitagorica lo ritroviamo adesso come fattore costante e arcano della superficie sferica.

La superficie della sfera, come scoprì e formalmente dimostrò Archimede, è sempre 4 volte l’area del suo cerchio massimo. Questo invariante, nella sua bellezza, è il massimo risultato della geometria del Siracusano.

I raggi fondamentali – o direzioni – della sfera sono 6, mentre le direzioni dello spazio piano sono 4. Ma il piano ideale infinito, generatore di ogni realtà e di ogni forma, si attualizza nella superficie sferica delimitante, senza perdere il suo valore dimensionale infinito di ordine 4.

Ecco perché sulla tomba di Archimede a Siracusa erano stati raffigurati insieme un cilindro e una sfera, col volume del cilindro che è 3/2 il volume della sfera inscritta. [Se il volume del cilindro è 33, 22 è il volume della sfera, 11 quello del cono: rapporti secondo la scala decrescente 3-2-1, come aveva dimostrato Archimede nella sua opera in due libri, Sulla sfera e il cilindro, che secondo Cicerone aveva rappresentato il suo capolavoro].

La sequenza discendente dal volume relativo del cilindro a quello del cono, passando per il volume intermedio della sfera, rispondeva anch’essa all’andamento della tetraktys: la misura relativa dei volumi dei solidi curvi puri era ugualmente continua.

La geometria di Archimede riflette il concetto di continuità dimensionale. Le forme curve erano comunque razionali. L’Universo spaziale era improntato alla geometria e la decade pitagorica ne esprimeva l’intima essenza. Il primato concettuale dei numeri naturali, quelli delle 10 dita umane, non era insidiato dalla perversione arcana di certi numeri irrazionali o trascendenti come radice di due e pigreco. In questo senso il grande Libro del Mondo era composto di numeri e figure geometriche, come dirà poi Galileo.

3* E’ bene chiarire, evitando equivoci, che Archimede giungeva alle sue impaccabili dimostrazioni solo e soltanto attraverso complessi e articolati procedimenti formali, rigorosi e impeccabili sotto il profilo dimostrativo: non poteva non essere così, per un vero matematico. Molto spesso utilizzando l’argomento per assurdo, dimostrando cioè che deve essere necessariamente così, perché diversamente si avrebbe una contraddizione, Archimede aveva intessuto di teoremi tutte le sue magnifiche opere. Tale logica binaria è quella stessa di Parmenide. Tra l’Essere e il ‘non essere’ non c’è alcuna alternativa. Il non essere è per forza un errore. L’Essere, che è il contrario di qualsiasi non essere, non può che essere. La verità è non può essere che se stessa. Ciò nonostante le dimostrazioni per assurdo saranno guardate con sospetto da un ramo della matematica moderna.

I trattati di Archimede sono costruiti in modo perfetto, ma egli non rivela mai da dove attinga quel “quid” che gli consente di elevarsi così in alto. Non rivela, cioè, la radice profonda delle sue intuizioni, sulle quali ha poi costruito il perfetto edificio formale delle sue impeccabili dimostrazioni, una di seguito all’altra, svolgendo tutti gli argomenti col procedimento tipico della geometria deduttiva e senza lasciare alcun vuoto.

Nel trattato sul Metodo meccanico, ritrovato nel 1906, si comprende invece che Archimede si è servito euristicamente di confronti, di pesature ideali, di piani di equilibrio, di centri di gravità, violando i dettami platonici per la geometria della riga e del compasso.

Vi era stato costretto dall’estrema difficoltà nel trattare il ‘curvo’ in assenza del calcolo infinitesimale moderno. I conoidi e gli sferoidi erano un altro arduo banco di prova.

Archimede non poteva prescindere da procedimenti di verifica, per così dire empirici o collaterali. Il trattato del Metodo era stato inviato ad Alessandria, a Eratostene, con tanto di lettera di accompagnamento, che però aveva quasi un sapore ironico. Archimede sembrava adesso rivelare i suoi trucchi, ma in realtà non svelava nulla. Infatti, egli aveva già comunicato ai matematici di Alessandria le proposizioni 14 e 15 del Metodo, senza fornire dimostrazioni, bensì invitando a trovarle. Altro non poteva essere se non un’ironica sfida oppure una sottile vendetta. Cioè, una provocazione.

Adesso, inviando il trattato sul Metodo, forniva anche le dimostrazioni di queste due sorprendenti proposizioni, di tipo esclusivamente geometrico e che non avevano nulla a che fare con gli altri esperimenti geometrici di tipo meccanico. Archimede aveva di nuovo confuso le acque ed è probabile che neppure questa volta Eratostene potesse aver compreso fino in fondo come Archimede avesse potuto raggiungere i suoi risultati.

Per quale scopo, come e perché, egli aveva ideato le meravigliose stranezze dell’unghia cilindrica e del cilindro a croce, sapendo già dove voleva andare a parare, per darne poi una dimostrazione formale, in relazione al volume del cubo contenente il cilindro ecc., ma non scoprendo mai le batterie?

Eratostene sarà rimasto deluso e interdetto. Archimede lo aveva preso in giro, come appunto sembra lasciar intendere, nella prefazione stessa al Metodo (cioè la lettera d’accompagnamento dell’opera inviata ad Alessandria), in cui si possono già cogliere sfumature ironiche, diplomaticamente velate.

L’aver introdotto nel Metodo [non un’opera geometrica, bensì l’esposizione di un sistema di ricerca: quindi strumento servente, che si deve presumere Archimede avrebbe utilizzato fin dal principio] delle proposizioni puramente geometriche, senza però indicare come fossero germinate e per quale scopo, ha un indubbio sapore di beffa.

Il Metodo, che possiede uno stile diverso dalle altre opere, costituirebbe una sorta di comunicazione privata. Archimede accenna subito a enunciati già inviati senza dimostrazione, con l’invito a trovarle. Che senso ha tutto ciò? Dall’andamento del Metodo si è costretti a dedurre che Archimede non si faceva troppa stima del “lettore” Eratostene. Ed è così vero che dopo aver mostrato – apparentemente – gli arnesi o presunti tali della sua ricerca, Archimede passa però ancora una volta alla geometria pura, con due teoremi che col Metodo meccanico non c’entrano nulla. Se non è questa una presa in giro, allora cos’è?

Il Metodo meccanico è del tutto inutile se non si comprende quanto già nasconde nel proprio seno. Ecco perciò un altro aspetto della “questionearchimedea”. Cioè la ricerca geometrica e la sfida. I risultati perfetti e il loro continuo enigma. Eratostene e i suoi matematici, ricevuto il trattato, avranno forse fiutato l’inghippo, ma non potevano comprendere. Archimede li stava portando in giro, li confondeva e al tempo stesso li annichiliva, li dileggiava. Egli soltanto era il grande Maestro della geometria tanto invocato da Platone. Il ‘platonico’ Eratostene, detto il signor Beta, riceveva una bella lezione dal signor Alfa di Siracusa, che stava molto meglio a casa sua.

LA QUESTIONE ARCHIMEDEA

1* Attilio Frajese, il traduttore italiano delle opere di Archimede, lo dichiara espressamente: << Si è a lungo parlato (e scritto) di una “questione archimedea”. Questi dimostra in modo impeccabile l’esattezza dei risultati, e la dimostrazione si compie spesso attraverso una rete intricata di proposizioni, ordinata però in modo assai preciso. Ma una tale dimostrazione presuppone che si conosca già il risultato: essa non ha alcun valore euristico, non conduce cioè a ‘trovare’, anzi presuppone che si sia già ‘trovato’. Si pone allora il problema di come Archimede abbia ‘trovato’ i risultati dei quali poi mirabilmente e rigorosamente dimostra la validità >>. Aggiunge Frajese: << Neppure il Metodo risolve completamente la questione archimedea >>.

Se utilizzando anche il metodo meccanico Archimede riuscì a predeterminare l’area del segmento parabolico, spiega Frajese, ciò non avvenne per la determinazione della superficie sferica.

Dunque, come fece per la sfera? Da dove vengono fuori quei numeri o rapporti semplici che sono il segreto di Archimede, come ad es. il rapporto 4/3 per il volume della sfera ecc.? Archimede conosceva già i suoi principali risultati che poi dimostrava rigorosamente ricorrendo a un impianto indiretto, fondato sull’argomento per assurdo. Come mai? Archimede non aveva truccato le carte. Tuttavia, non si lasciava penetrare, comportandosi quasi come un mirabolante prestigiatore.

Stiamo cercando di capire come abbia fatto. Tentiamo cioè di scoprire le ‘sue’ carte. Per far questo dobbiamo risolvere il “segreto” racchiuso nell’ideazione dell’unghia cilindrica e del cilindro a croce, i due enunciati con i quali aveva sfidato Eratostene, accolti acriticamente da molti addetti ai lavori, quando al contrario vi era fondata materia per dubitare, non del genio di Archimede, ma dei metodi di cui si serviva e delle sue relazioni con i saccenti matematici alessandrini.

Per afferrare il senso recondito del Metodo meccanico, che poteva aver dato l’illusione a Eratostene di aver afferrato i segreti del Siracusano, è necessario capire il “trucco”. Archimede aveva nuovamente disorientato Eratostene e i matematici alessandrini facendo comparire all’improvviso due nuovi solidi, che uscivano misteriosamente dal suo cervello come conigli da un cappello a cilindro, sbattendogli ora in faccia le dimostrazioni. Viceversa, come aveva fatto Archimede a idearli, cioè a costruirli in quella maniera [la matematica di Archimede è costruttiva], e perché lo aveva fatto, visto che stava adesso rivelando un metodo sporco, il metodo meccanico fatto di pesature ecc., per essere un matematico platonico e un purista?

Dobbiamo capire vedere che per Archimede non c’erano confini tra l’ideare e il fare, tra il geometra puro e il meccanico. E questo è un pitagorismo allo stato puro, come nell’analogia musicale dei martelli di Pitagora… Potremmo anche aggiungere che l’occhio e l’idea, in Archimede, avevano una forza congiunta portentosa, la medesima potenza di un artista rinascimentale o di un grande scienziato moderno. E dicendo così, crediamo non di svelare nulla di nuovo, ma far risaltare quell’alone magico che ha sempre circondato la sua figura già dalle fonti antiche.

Plutarco lo definiva perennemente in preda al canto delle sirene. La mente di Archimede possedeva qualcosa in più di un’eccezionale mente matematica. In lui si potrebbe cogliere un’affinità con lo stesso atteggiamento di Ramanujan, il grande matematico indiano autodidatta che intuiva meravigliosamente, prima di ogni dimostrazione, tutto dedito alla sua piccola dea, Namagiri, come Archimede – secondo Plutarco – lo era per la sua domestica Musa. Il genio naturale di Ramanujan si avvicina assai a “Archimede pitagorico”, capace di concepire a tavolino problemi mostruosi e immensi, come quello dei Buoi delSole. La mente umana è un capolavoro divino della natura. La natura è a sua volta un’impronta divina. Lo Spirito aleggia sulle cose, Pitagora e Platone ne erano consapevoli. Epicuro (341 – 270 a.C.), che è piuttosto una presenza attuale nel mondo scientifico moderno, non contagiò Archimede.

2* A proposito di Archimede e della “questione archimedea” dovremo parlare anche di piramidi e di coni, e persino di ‘piramidine’ incastrate in un cubo.

Abbandoniamoci però a una digressione. In fondo questi appunti sono stati concepiti come una serie continua di digressioni, legate tuttavia da una conclusione per nulla trascurabile, quale sia stato il percorso seguito.

La grande piramide di Cheope (Cheope è “colui che appartiene all’orizzonte”), orientata sui 4 punti cardinali con la massima precisione, è stata costruita in proporzioni tali “da non gettare ombra”: La mole di queste costruzioni, poiché salgono a grande altezza, si restringe molto lentamente, e fa svanire anche l’ombra, secondo un principio della meccanica (Ammiano Marcellino, Historiae, XXII, 15, 28 segg.) La sfida dell’ombra è un archetipo delle civiltà solari, con tutte le sue valenze simboliche. Napoleone si riposò all’ombra delle piramidi, sotto 40 secoli di storia, accompagnato dal matematico Monge, che aveva sistemato la geometria proiettiva di Desargues. Le piramidi sono collegate al culto solare. Rappresentavano la vita dopo la morte.

Scrive Plinio (Naturalis Historia, XXXIII, 82): Il metodo per calcolare l’altezza delle piramidi e misure analoghe fu escogitato da Talete di Mileto: misurava la lunghezza dell’ombra che viene proiettata all’ora in cui è di dimensioni pari a quella del corpo che la proietta.

L’ora era quella in cui, nella località presa in considerazione, l’altezza del sole sull’orizzonte era di 45 gradi (formando l’ombra dello gnomone un triangolo rettangolo con i cateti uguali).

Talete, secondo Erodoto, avrebbe predetto la data di un’eclisse di sole, per una battaglia tra i Lidi e i Medi, che intimoriti dal fenomeno, la interruppero. Si pensa che tale eclisse sia avvenuta il 28 maggio del 585 a.C. (la cronologia antica è questione assai difficile). A noi interessano anche le eclissi di sole e di luna, non solo per il cono d’ombra che permise ad es. di valutare il rapporto tra il raggio terrestre e quello lunare nelle eclissi di luna, e le suggestioni che tali fenomeni indubbiamente provocano, perfino a riguardo del terribile problema bovino di Archimede.

Poiché siamo in argomento di piramidi, va annotato che dopo Plinio, anche Diogene Laerzio, nelle Vite dei filosofi, riporta l’episodio di Talete in Egitto, riprendendolo molto probabilmente dalla fonte originaria: Ieronimo poi afferma che egli misurò le piramidi, basandosi sulla loro ombra, dopo aver osservato in quale momento la nostra ombra è uguale all’altezza. Talete si reca in Egitto (come aveva già fatto Pitagora e come poi faranno altri greci), e egli qui apprenderebbe le basi della “geometria”, frequentando i sacerdoti egiziani. In Egitto avrebbe fornito una bella prova del suo genio, risolvendo in un modo semplicissimo e brillante, quello che nel raccontino sembrerebbe, per implicito, essere stato un ‘problema’ su cui i suoi maestri egiziani o i maestri dei tali maestri che avevano le piramidi davanti agli occhi tutti giorni, avevano forse già risolto in quel modo? L’aneddoto è carino, ma è assurdo. Abbiamo già visto perché. Le piramidi erano antichissime già all’epoca di Talete e sappiamo dal racconto di Diogene che non avevano raccontato nulla dei loro segreti: se mai, i sacerdoti egizi avevano soltanto scherzato, con Talete, che doveva essere una specie di mercante-viaggiatore greco, intelligente e curioso, ma senza una grande civiltà alle sue spalle. Indubbiamente esiste il mistero delle Piramidi (monumenti celesti), e l’enigma delle civiltà antiche, probabilmente molto più antiche di quanto immaginiamo (secondo Diodoro Siculo, che scriveva circa 2 mila anni fa, la civiltà egiziana risaliva 15 mila anni prima).

Talete avrebbe scritto due sole opere, Sul solstizio e Sull’equinozio, decretando che le altre questioni sonoinafferrabili. Talete sarebbe stato uno dei fondatori della geometria greca, se non il fondatore, prima di Pitagora. “Il triangolo è la figura dell’ombra e il geometra antico è una mente che vede dappertutto triangoli”(R. Casati, op. cit., pag. 97).

Il Demiurgo del Timeo potrebbe avere ascendenze simili, ben inteso di origini astronomiche. A parte tutto, come fece Talete a misurare l’ombra delle piramidi? Preferiamo ripeterci, con qualche aggiunta, perché uno degli scopi di questi ‘appunti’ è cercare di inquadrare la genesi ideativa del mostruoso problema bovino inviato da Archimede al platonico Eratostene, che era soprattutto un grande filologo omerico, ma anche ai matematici alessandrini del Museo.

Talete che per primo iscrisse nel cerchio il triangolo rettangolo e che per questa scoperta sacrificò un bovino? E la grande piramide che cela la sua altezza, ma anche la propria base, in un ammasso di pietra, e con ciò una parte dell’ombra che servirebbe a Talete? Quando il sole è a 45 gradi nel cielo, l’ombra della punta della piramide cade al proprio interno, come aveva spiegato Ammiano Marcellino (questa è già ‘trigonometria’). Il paradosso è che ciò che si deve già sapere per potere misurare l’altezza delle piramidi ricorrendo al metodo dell’ombra, basta anche per misurarle senza ricorrere a questo metodo.

Procedendo dalle eclissi di sole, servendosi poi di altri metodi, Aristarco tentò di calcolare il rapporto tra la distanza terra-sole e la distanza terra-luna.

Nell’Arenario, Archimede si riporta a queste osservazioni, avendole ripetute egli stesso dopo suo padre e avendole perfezionate ulteriormente. Ciò che conta è che le distanze del sole e della luna sono state ancorate alla dimensione della terra, cioè al suo diametro e alla sua circonferenza.

Senza riflettere sulle ombre non c’è modo di immaginare che il sole sia così distante della terra e ne sia totalmente più grande. Le stime antiche, anche quelle di Archimede, erano sbagliate a causa dell’estrema difficoltà pratica nella misurazione di un angolo piccolissimo, appena leggermente inferiore a un angolo retto, formato dal trigono terra – sole – luna. [Il Sole dista dalla Terra più di 10.000 diametri terrestri].

Per noi persone comuni del tempo moderno, che è un’epoca assolutamente complessa in tutti i sensi, è una bella e istruttiva lezione vedere che in antico si verificavano episodi affini o identici a quelli che accadrebbero oggi, circa le distanze tra il senso comune e la scienza, come nel caso del povero Talete, che del tutto ignaro dei segreti della grandi Piramidi di Giza, credeva di potersela cavare con l’idea abbastanza intelligente dell’ombra dello gnomone, oppure al contrario le ironie di Archimede nei confronti degli Alessandrini. L’aspetto psicologico di queste situazioni è perfettamente identico. Ed è il trionfo del sapere all’interno però della buona e ripagata modestia. Lo scherzo vitale e la verità: tutto quanto ‘a misura d’uomo’. Archimede non doveva spiegare come facesse a conseguire i suoi risultati. Il genio non è un fatto di organizzazione collettiva, e importavano le dimostrazioni oggettive, non da dove essere derivassero. Ognuno ha i suoi segreti. Il bello è che la curiosità vorrebbe sempre sapere di più, ma per questo bastava cercare di capire come Archimede avesse potuto allestire quelle sue magnifiche dimostrazioni, senza dover rivelare i ‘segreti’ del mestiere (è la stessa situazione di un prestigiatore che dovesse spiegare al pubblico i suoi trucchi). Archimede qui tiene un ruolo di antica sapienza, affine a quello dei sacerdoti egiziani nei confronti del povero Talete, alias nei riguardi di Eratostene e dei matematici alessandrini. La grande Piramide sorriderebbe. Ma noi comuni moderni siamo curiosi, anche se abbiamo ormai scordato le formule scolastiche della sfera, anzi nelle scuole elementari le applicavamo correttamente, senza che nessuno ce le avesse mai spiegate veramente. [Per analogia, questo vale in genere anche nella matematica e la fisica dei licei, e forse anche per tutto il resto: ‘capire’ è una faccenda alla quale si è spasso rinunciato in nome del ‘fare’, che pure conta].

L’UNGHIA DEL LEONE E IL CILINDRO A CROCE

1* Due proposizioni del Metodo meccanico, la proposizione 14 e la proposizione 15, sono particolarmente significative, ma alquanto misteriose. Sono gli enunciati che Archimede aveva in precedenza inviato ad Alessandria, invitando a trovarne la dimostrazione. Eratostene non ci era riuscito e doveva aver chiesto lumi a Siracusa. Adesso Archimede gli risponde, in maniera apparentemente completa ed esauriente, esponendo dapprima il metodo meccanico seguito in generale per i suoi modi di procedere nei casi geometrici più difficoltosi, alludendo al fatto che è sempre bene avere a disposizione qualche nozione preventiva circa le cose ricercate e che saranno rese oggetto di vera e propria dimostrazione. Un conto è ottenere degli indizi, altra cosa è la dimostrazione (ad es. Democrito non possedeva la dimostrazione del volume della piramide, pur sapendo che doveva valere 1/3 il volume del cubo in cui la piramide a base quadrata era inscritta, a differenza di Eudosso che ottenne invece una dimostrazione generale per il volume di tutti i tipi di piramide).

Archimede inviava ad Alessandria enunciati sprovvisti di dimostrazione. Altre volte aveva addirittura inviato dei falsi enunciati. E’ evidente che lo facesse apposta. Mai avrebbe ingannato un carissimo amico come Conone di Samo. Se così aveva fatto, una ragione ci doveva essere. La ragione consisteva nella boria del Museo, da cui Conone stesso si era dovuto guardare, prima di morire ancora giovane.

Rivolgendosi a Eratostene, che doveva avergli chiesto chiarimenti, lo definisce senz’altro come diligente ed egregio maestro difilosofia, e tale anche di apprezzare nella matematica le teorie dimostrative. Perciò Archimede non gli riconosce un vero e proprio ruolo di addetto ai lavori, bensì soltanto di cultore. Il che già mette sull’avviso, a differenza di come aveva giudicato Conone, valentissimoed espertissimo.[Il trattato sul Metodo risale a un periodo successivo alla morte precoce dello stimatissimo astronomo Conone, suo carissimo amico].

In queste espressioni misurate ma nette di Archimede per Eratostene c’è una punta di diplomatica ironia, che si accentua notevolmente nella sostanza delle cose.

Non solo il Metodo non spiega bene come facesse Archimede a raggiungere le sue dimostrazioni, anche se “lascia veder dentro (meglio sarebbe stato dire sbirciare) l’officinamatematica” del Siracusano, come asserì Zeuthen [cioè, una matematica dietro le quinte]. Il Metodo lascia insoddisfatti perché non ha un preciso valore euristico: non conduce – infatti – a trovare un risultato, ma permette di dimostrare rigorosamente l’esattezza di un risultato al quale si sia giunti per altra via (Attilio Frajese).

Secondo Dijksterhuis, il Metodo va considerato come una comunicazione privata a Eratostene, piuttosto che come un trattato destinato alla pubblicazione. [Tuttavia il Metodo ci è pervenuto ugualmente, perché fu più volte ricopiato e poi trasferito nel codice C, che conteneva anche lo Stomachion].

Osserva Frajese che si dovrebbe dedurre che Archimedenon facesse troppa stima del “lettore” Eratostene.

Il palinsesto del Metodo meccanico s’interrompe sul più bello, all’inizio della proposizione 15. Il primo enunciato, la proposizione 14, riguarda il volume dell’unghia cilindrica, pari a 1/6 di quello dell’intero parallelepipedo o cubo di riferimento. Il secondo enunciato, proposizione 15, riguarda il cilindro a croce, il cui volume è pari a 2/3 di quello del cubo contenente.

“Perché”, e “come”, Archimede ideò questi stranissimi solidi? La domanda è inevitabile. E come aveva fatto a concepirli se non conosceva già in anticipo il loro scopo, il che equivale a dire che doveva conoscere già intuitivamente il risultato da dimostrare?

E’ il classico serpente che si morde la coda. Ed ecco, dunque, il senso quasi beffardo del trattato sul Metodo nei riguardi del destinatario Eratostene e dei suoi matematici, che ben difficilmente avrebbero potuto afferrare l’arcano, poiché non avevano saputo risolvere i due enunciati che gli erano stati già proposti. Archimede ora inviava le sue dimostrazioni, che erano di tipo geometrico, ma lo faceva in un contesto di tipo “meccanico”, estraneo alla situazione. Le prime 13 proposizioni del Metodo erano dunque fuorvianti o fuor di luogo. Siamo perciò costretti a supporre una sottilissima presa in giro. Eratostene era stato sminuito, anche se nella premessa al Metodo si ricorreva nei suoi confronti a eufemismi.

L’unghia cilindrica, chiamata da Cavalieri unghiata del leone *[Bonaventura Cavalieri conosceva già il Metodo?], è un solido curvilineo ottenuto tagliando diagonalmente un cilindro a partire dal centro del cerchio superiore e scendendo GIù fino al punto estremo della base, terminante perciò in un punto ideale. La forma così ottenuta è proprio quella di un’unghia. L’unghia cilindrica è chiaramente un’invenzione, un solido ideato ad hoc: delimitato da un semicerchio, da una semiellisse, e da una superficie cilindrica.

Con questo solido Archimede aveva trovato il collegamento, la possibilità del confronto o il termine di paragone tra il retto e il curvo (una delle dicotomie pitagoriche). Non bastava. Occorreva qualcosa di più.

Con il cilindro a croce, correlato a un cubo, in cui idealmente erano forzati a coesistere due cilindri incastrati l’uno nell’altro in direzioni opposte, il geniale Archimede otteneva un’altra pietra di paragone – un elemento ulteriore – sul misterioso rapporto tra ‘retto’ e ‘curvo’. I due stranissimi solidi da lui ideati sono complementari a tale scopo. Il lettore potrà recuperare su Internet molte altre notizie sulle accennate proposizioni 14 e 15 del Metodo, e potrà anche trovare delle figure idonee che rappresentano e spiegano a sufficienza la conformazione altrimenti sfuggente di questi due solidi di Archimedei.

*Da parte nostra facciamo riferimento alle immagini presenti in G. Loria (Lescienze esatte nell’antica Grecia, Hoepli ristampa, pag. 327) e in P. D. Napolitani (Archimede, Le Scienze 2001, pag. 53), soltanto per l’unghia cilindrica. Mentre l’unghia cilindrica è facile da visualizzare, saper ‘vedere’ il cilindro a croce è più difficile.

2* Per intendere quest’aspetto fondamentale che dovrebbe appartenere agli inizi della ricerca geometrica del Siracusano e non tanto all’età matura, alla quale il Metodo risalirebbe temporalmente, in relazione a Eratostene, occorre indovinare come fece a ideare questi solidi del tutto inusitati. E se dunque Archimede aveva ideato i due solidi, il Metodo in questo caso non serviva a niente. Non aveva alcun valore nemmeno a livello puramente indicativo. Ne consegue una presa in giro e un nascondimento.

Il volume dell’unghia cilindrica – o unghia del leone – è pari a 1/6 del volume del cubo che contiene il cilindro retto. Il volume della croce cilindrica è pari a 2/3 del volume del medesimo cubo riferibile. Ed ecco come Archimede descrive i due solidi partoriti della sua mente geniale.

Unghia cilindrica: S’inscrive un cilindro in un parallelepipedo (abbiamo però preferito il cubo), con le basi coincidenti e la superficie laterale tangente alle facce. Si conduce un piano diagonalmente, passante per il centro di una delle basi e un lato della base opposta. Si staccherà così dal cilindro inscritto nel cubo, (con questo taglio) una porzione limitata deal piano secante, dal piano della base e da una parte della superficie cilindrica (unghia cilindrica). Il suo volume sarà pari a un sesto di quello del cubo (che qui dobbiamo considerare soltanto idealmente, mentre i taglio è stato operato concretamente sul cilindro contenuto nel cubo (vedi figura 2).

Cilindro a croce. In un cubo s’iscrive prima un cilindro con le basi inscritte in due facce opposte e la superficie laterale tangente alle altre quattro. Poi si inscrive un secondo cilindro analogo, avente adesso per basi le altre due facce opposte e la superficie laterale tangente alle altre quattro (doppio cilindro forzato a croce). Il volume del cilindro a croce sarà pari a 2/3 del volume del cubo di riferimento.

L’unghia cilindrica è stata ricavata dalla sezione diagonale di un cilindro, a partire dal centro della sua faccia superiore. Se sezioniamo due volte il cilindro, una volta per ciascun lato, otterremo due unghie cilindriche. Ciò che resta, è un solido di risulta, formato da una base circolare, da due facce laterali piane (quelle del taglio) e da una sottile costola cilindrica per ogni lato verticale che va rastremandosi dal basso verso l’alto. Se avessimo a disposizione un budino a forma cilindrica, operati i due tagli laterali in diagonale, giù a scendere fino alla base opposta, il procedimento si rende evidente. Dal solido risultante, tolte le due unghie, si può ottenere, con altri due tagli a scendere sui lati curvi, una piramide che rispetto al parallelepipedo che la contiene avrà il valore relativo di 1/3 già noto agli atomisti ionici e dimostrato da Eudosso. Archimede prestigiatore ha rettificato il solido curvo. Il volume della piramide è 1/3 del volume del cubo, ed è il doppio del volume dell’unghia cilindrica. Lo scherzo per Eratostene e i matematici alessandrini è evidente.

Ritornando ai tagli che portano all’unghia cilindrica, vuol dire che tutti gli altri scarti, le due unghie cilindriche in aggiunta agli altri residui, hanno un volume pari a 2/3 del parallelepipedo. Eravamo però partiti da un cilindro, e non da un solido retto, il cubo o il parallelepipedo contenente, che tuttavia è il riferimento. Cilindro e cubo contenente, nel caso di cilindro retto, non hanno tra loro alcuna relazione: se ad es. assegniamo al cubo il valore 42, il cilindro varrà qualcosa che si avvicina a 33, ma non esattamente tale valore intero. Invece l’unghia cilindrica è ideata e costruita appositamente perché il suo volume possa essere perfettamente correlato a quello del cubo: se il cubo vale 42, allora l’unghia vale 7

Non scordiamo il cilindro a croce, cioè i due cilindri forzati l’uno nell’altro, entro un cubo.

Ogni cubo contiene 6 piramidine di Saunderson *[cioè il matematico cieco, chetenne la cattedra “lacasiana” dopo Newton, menzionato nella Lettera a uncieco di Diderot]. Ogni pirimidina vale 7, se tutto il cubo vale 42.

Equivalendo l’unghia cilindrica alla sesta parte del volume del cubo di unitario riferimento, in cui è stato iscritto il cilindro di partenza, ciò significa che equivale al volume di una ‘piramidina’ di Saunderson, che in numero di 6, corrispondente alle 6 facce del cubo, ne compongono anche il volume.

Si assiste cioè al meraviglioso passaggio dalla dimensione piana di valore 2 a quella solida di valore 3 e infine al passaggio dal ‘retto’ al ‘curvo’.

*[Il valore 7 è stato assegnato in relazione a ciascuna delle 6 facce del cubo. Il cubo, svolto su un piano, ha 6 facce: quante, appunto, le 6 piccole piramidi che incastrate tra loro, formano il cubo riempiendolo perfettamente].¹

Archimede aveva già stabilito nella Misura del cerchio che il rapporto d’area tra il quadrato circoscritto e il cerchio inscritto nel quadrato è all’incirca 14/11. Ed è lo stesso ordine del volume della piramide retta 14 (rispetto al cubo 42) e del valore solido del cono rispetto alla sfera (11/22) oppure del cono rispetto al cilindro (11/33). A tali risultati, formalmente dimostrati, Archimede era giunto in un’altra opera, La sfera e il cilindro, con rigorosa e articolata serie di dimostrazioni. Tuttavia questi rapporti potrebbero essere sintetizzati tramite un’analogia: come l’area di un rettangolo isoscele, inscritto in un quadrato, vale la metà dell’area del quadrato, così aumentando di una dimensione, passando cioè dal piano bidimensionale alla terza dimensione dei solidi, l’invariante geometrico segue il medesimo rapporto.

Il volume della piramide è la terza parte del volume del parallelepipedo contenente, e il volume del cono è analogamente la terza parte del volume del cilindro che lo contiene.

Il passaggio dal valore a due dimensioni pari a 1/2, al valore tridimensionale dei solidi cioè 1/3, non rappresenta altro che l’applicazione del principio della continuità dimensionale espresso dalla tetraktys. Tale invariante vale anche per la sfera, il cono e il cilindro nei loro reciproci rapporti. Tali solidi ‘curvi’ sono posti tra loro nel rapporto di 1 per il cono, di 2 per la sfera e di 3 per il cilindro, secondo le rigorose dimostrazioni formali di Archimede, alle quali però si poteva arrivare con l’intuizione dimensionale e in analogia con i solidi retti, il cubo e la piramide.

Il caso della sfera, il cui volume vale 2/3 rispetto a quello del cilindro, è un caso nuovo. Poiché tra il volume 3 del cilindro si poneva in origine il volume 1 del cono, e dato che la sfera è ragguagliabile al cono, in quanto le sezioni orizzontali di ciascun solido sono comunque dei cerchi (che si rastramano fino al punto ‘zero’ del vertice ideale del cono), secondo il principio di continuità dimensionale, che è invariante, si ottiene immediatamente che il volume della sfera è necessariamente intermedio tra quello del cilindro e quello del cono, secondo la sequenza razionale crescente dei numeri 1-2-3. Gli indivisibili di Cavalieri era concetti impliciti in Archimede, del resto già presenti alla scuola pitagorica della Magna Grecia.²

La tetraktys pitagorica ha continuato a svolgere il suo ruolo. Se il suo vertice rappresentava il segmento di valore dimensionale 1, la seconda fila dava il valore dimensionale 2 dell’aera delimitata, la terza fila il valore 3 dei solidi, la quarta fila il valore 4 della superficie sferica.

Il Demiurgo di Platone avrebbe potuto attribuire al punto senza dimensioni il valore zero, ma lo “zero” non era considerato come cifra dai Greci, quando per i pitagorici contavano solo i numeri naturali, che difatti permettevano i rapporti razionali dell’armonia musicale. Tale armonia doveva essere contenuta e rispettata anche nelle forme dei solidi ideali. Così era in realtà, e questo lo dimostrò Archimede pitagorico, perennemente incantato dalla sua Sirena, rapito nella musica delle sfere.

*[Il sogno di Scipione in Cicerone, nel De Republica, troverà una grande eco nel grande commentario fattone da Macrobio nel V secolo, l’età fatale del declino dell’Impero romano d’Occidente, mentre le Muse si ritroveranno tutte quante nelle Nozze di Filologia e Mercurio, opera composta nello stesso periodo da Marziano Capella: sappiano gli studenti quanto ricco fosse il mondo antico].³

3* Se al cilindro assegniamo il valore 33, il volume della sfera varrà 22 e quello del cono 11. Abbiamo così riassunto i segreti intuitivi di Archimede, impliciti ad alcune sue fondamentali opere geometriche. Ma la relazione tra ‘retto’ e ‘curvo’ rimane incommensurabile poiché il valore di “pigreco”, ricompreso nel limite delle frazioni 22/7 e 22/71 [il limite superiore di 22/7 corrisponde al rapporto tra il valore del volume della sfera rispetto al cilindro e a quello del volume dell’unghia cilindrica rispetto al parallelepipedo o al cubo contenente il cilindro da cui è stata ricavata], è un numero irrazionale e per di più trascendente come si sa dal 1882.

Il ‘retto’ e il ‘curvo’, figli della medesima Dea o Musa della Geometria (ovvero ambedue figli del piano infinito), non sembravano appartenere alla medesima famiglia. Archimede compì il miracolo. Trovò quel collegamento razionale, aritmetico e pitagorico, invano cercato in precedenza. L’armonia dell’Universo era salva. Il Cosmo era “razionale” corrispondendo al “logos”. Archimede era il grande maestrodellageometria invocato da Socrate nella Repubblica di Platone

Nel cilindro a croce la forzatura ideale di due cilindri retti in un cubo (ma in direzioni sfasate di 90 gradi) lascia ‘scoperte’ soltanto 2 facce del cubo, mentre impegna le altre 4 facce in direzioni opposte. Il cubo in questione è totalmente riempito da 6 piccole piramidi di Saunderson di valore solido 7, mentre i due cilindri, separatamente l’uno dall’altro, equivalgono a loro volta a 6 coni.

Dal momento che i due cilindri in questione sono forzati l’uno nell’altro in un cubo 42 e da opposte direzioni (“a croce”), viene meno un certa dose di volume.

Il medesimo cubo 42 (cioè 7 x 6) è composto da 6 piramidine di valore 7 ovvero da tre piramidi grandi di valore 14, mentre il volume del “cilindro acroce” impegna soltanto 4 facce del cubo su 6, lasciandone 2 scoperte (una in alto e l’altra in basso), del tutto ‘immutate’. Sarebbe vano ragionare in base al rapporto tra l’area del quadrato e l’area del cerchio inscritto (equivalente a circa 14/11), perché ‘retto’ e ‘curvo’ non dialogano tra loro in questo modo.

La compressione degli spazi, dovuta alla forzatura ideale di un cilindro entro l’altro, a forma di croce, non è esprimibile in questa maniera.

Ma se ci rifacciamo alla relazione analogica, tipica del cubo, per cui le sue 6 facce corrispondono alle 6 piramidine (ciascuna di valore solido 7) che lo compongono, scalando di una dimensione avremo modo di individuare un invariante che ci condurrà a risolvere il mistero del volume del “cilindro a croce” che infatti impegna soltanto 4 facce delle 6 facce del cubo.

Il rapporto solido tra il cubo 42, e il cilindro a croce di volume X che è l’incognita cercata, è pari a 6/4. Quindi, in un cubo 42 (cioè 6 x 7), il “cilindro a croce” ha un volume razionale correlabile a quello del cubo, pari 28 (cioè 4 x 7). E notiamo pure che 28 è un numero pitagorico perfetto, somma dei suoi divisori (per significare meglio che Archimede era veramente un pitagorico).

La dimostrazione formale di questo enunciato di Archimede (proposizione 15) manca nel palinsesto del Metodo meccanico, che proprio qui s’interrompe, come in un “trilling”. Ovviamente non era quella, qui indicata, per analogia.

Quest’analogia è però fondata ed è fondante: germogliò così, nella mente di Archimede, permettendogli di presagire intuitivamente il risultato. I nostri accenni al “pensiero trasformativo” sono corretti.

Il valore relativo tra il volume del “cilindro a croce” e il volume del cubo che lo contiene si pone nel rapporto da 4 a 6, pari a 2/3. La differenza di volume tra i due solidi è uguale a 14, cioè è pari al valore di una piramide grande oppure di due “piramidine di Saunderson”, il matematico della Lettera del cieco di Diderot.

Questo invariante geometrico, di tipo analogico, ha consentito al Siracusano il primo passo intuitivo per il ragguaglio tra il ‘retto’ e il ‘curvo’ che sembravano apparentemente estranei l’uno all’altro.

Il secondo passo è dato dall’altro enunciato del Metodo, la proposizione 14, in base alla quale Archimede aveva affermato che il volume dell’unghia cilindrica equivale alla settima parte del volume del cubo oppure del parallelepipedo che contengono il cilindro. Qui interessa soltanto il cubo.

Eravamo rimasti, dopo tutti i tagli effettuati a proposito dell’unghia cilindrica, a una piramide di risulta, pari a 1/3 del cubo o del parallelepipedo (fa lo stesso) che contenevano il cilindro. Operati tutti i progressivi tagli del cilindro (o budino cilindrico nel nostro esempio), tagli simmetrici tra loro, fatti due a due, che portano alla piramide 14 come ‘risulta’ centrale, dovuta agli scarti, si deve giungere alla conclusione che quanto è stato già tolto deve valere i 2/3 del volume del cubo contenente, comprendendo il residuo del cilindro e la parte del cubo.

Questo valore 14 della piramide è la metà del valore solido del cilindro a croce rispetto al cubo 42. Ed è il dato che ci interessa. Il resto può essere trascurato, facendo presente che cerchiamo di stabilire per conto nostro il valore solido dell’unghia cilindrica rispetto al cubo e non rispetto al cilindro che Archimede sa già, prima di darne una formale dimostrazione, essere pari a 1/6 del volume del cubo. In altre parole, stiamo cercando di scoprire uno dei massimi segreti di Archimede, trascurando le dimostrazioni formali degli enunciati 14 e 15 del Metodo. Il palinsesto del Metodo s’interrompe alla proposizione 15. Il resto è andato perduto.

Nella prefazione di quest’opera indirizzata a Eratostene Archimede sembra voler ironizzare sullo zelante scienziato alessandrino, distinto filosofo e grande ammiratore delle ricerche matematiche. Archimede chiarisce nella lettera di premessa che questi teoremi sono d’un genere del tutto diverso da quelli che aveva in precedenza comunicati a Eratostene *[secondo Gino Loria, si alluderebbe Ai conoidi e sferoidi, che invece portano l’intestazione a Dositeo]. Archimede aveva già inviato a Eratostene i due medesimi problemi delle proposizioni 14 e 15 del Metodo, invitandolo a risolverli. Eratostene non c’era riuscito. Archimede gli invia le dimostrazioni, spiegando in chiave euristica il suo metodo meccanico: il che, come abbiamo detto, ha il sapore di una rbeffa o di una presa in giro. In realtà Archimede non svela nulla, ma sembra divertirsi a mescolare le carte. In questo medesimo contesto, cita Eudosso, a proposito del cono, della piramide, del cilindro, e del cubo. Stiamo ripetendo lo stesso concetto. L’intenzione di Archimede è apparentemente quella di fornire a Eratostene un metodo sicuro, ma ecco che ha inquinato le acque. Le proposizioni 14 e 15 del metodo derivavano da un geniale atto creativo che lasciava intendere di conoscere già intuitivamente il risultato che si era proposto.

Ancora peggio, si dovrebbe così presupporre per il terrificante problema bovino, indirizzato a Eratostene e ai matematici alessandrini. Si voleva distruggerli con un problema impossibile per i mezzi di calcolo di quel tempo.

Se Eratostene aveva capito poco o nulla dell’enunciazione dei due teoremi che gli saranno poi spiegati nel trattato sul Metodo, come avrebbe potuto risolvere il problema bovino, il cui primo risultato a stento può essere contenuto da un volume di 600 pagine? E’ evidente che Archimede aveva uno scopo preciso, ma non apertamente dichiarato, nel proporre quell’immane problema. Qui la sfida si risolve in uno sberleffo. Altro che stima e amicizia. Doveva esserci una ragione tremenda: ma quale? Ci torneremo sopra, a conclusione di questi appunti. Intanto proseguiamo nell’esposizione extra ordinem sulle intuizioni di Archimede.

4* Non stiamo dando numeri, ma i numeri o rapporti semplici di Archimede. In altre parole, stiamo spiegando la questione archimedea. Lo scarto di volume tra cubo e cilindro a croce è razionale. E’ invece irrazionale lo scarto di volume tra il cilindro e il cubo. Tutto s’aggiusta con l’unghia cilindrica. Adesso le famiglie dei ‘retti’ e dei ‘curvi’ hanno trovato un termine di dialogo. Il segreto sta nello stesso salto dimensionale del mito della caverna nella Repubblica di Platone. Nessuna relazione tra l’unghia cilindrica e il cilindro a croce. Tutto è stato mediato e unificato attraverso il cubo, che unifica le proposizioni 14 e 15 del Metodo (fa lo stesso nel caso del “parallelepipedo”, con riguardo all’unghia cilindrica).

Il segreto del volume relativo dell’unghia cilindrica stava nell’ invariante da una visione bidimensionale alla realtà tridimensionale. Archimede ha ideato l’unghia cilindrica poiché nella sua sezione mediale bidimensionale, essa non si distingue in nulla da un triangolo. Tale invariante è lo stesso del triangolo isoscele inscritto nel quadrato (rapporto di superficie di ½).

Nel salto dalla seconda alla terza dimensione sappiamo già che il rapporto si eleva da 1/2 a 1/3 seguendo uno stesso criterio che è il medesimo per la famiglia dei retti (piramide) e per la famiglia dei curvi (cono).

In sezione mediana, cubo e cilindro sono indistinguibili. Il soverchio (per usare la stessa immagine di un sonetto di Michelangelo circa il marmo e la statua), che abbiamo tolto dal cubo per arrivare alla piramide, ha un riscontro analogico col soverchio tolto al cilindro per giungere al cono.

Se prendiamo un quadrato ovvero la sezione verticale del cubo notiamo che essa è composta da 4 triangoli uguali. Anche nella terza dimensione tale rapporto di volumi si deve conservare secondo la regola già vista. Infatti, è così. La piramide – oppure il cono di risulta: fa lo stesso – dopo tutti i tagli impegnano la terza parte del volume dei rispettivi solidi, cubo e cilindro, indistinguibili in sezione piana verticale. Il rapporto è cresciuto a 3 a 1, mentre nella prospettiva piana o bidimensionale la sezione dell’unghia cilindrica corrisponde alla quarta parte del quadrato. Negli scarti, dovuti ai vari tagli, quella parte dell’unghia cilindrica (le unghie ricavabili sono 2) rispetto al cilindro da cui è stata tratta, equivale alla quarta parte dello scarto stesso rispetto a cubo. Se lo scarto complessivo era 28, l’unghia cilindrica vale 7. Ciò è tanto vero che la piramide risultante (tolto tutto ciò che attiene ai tagli simmetrici nel cilindro) ha valore 14. L’elemento univoco di correlazione è la piramide. Pertanto il volume dell’unghia cilindrica è la quarta parte dello scarto del cubo e vale 1/6 del suo volume.

Assegnando al cubo il valore 42, allora l’unghia vale 7. E si può scorgere un bel panorama secondo i seguenti punti: 1) Archimede sapeva già come operare; 2) ha identificato l’invariante su cui operare ; 3) l’unghia cilindrica e il cilindro a croce sono i suoi due strumenti di paragone; 4) il metodo meccanico è assente; 5) l’unghia cilindrica e il cilindro a croce sono autentici “conigli” estratti dal “cappello” di un grandissimo “prestigiatore”; 6) i due solidi sono stati costruiti ad arte, con intuizioni geniali: nel primo caso, per tagli e per scarti, nel secondo caso per compressione di spazi; 7) il procedimento è però il medesimo, rispondente al principio della convergenza verso uno scopo; 8) Archimede si è comportato come un pitagorico.

Se vogliamo una riprova di quanto affacciato prendiamo i valori frazionari dell’unghia cilindrica, 1/6, e del cilindro a croce, 2/3 [sempre con riguardo allo stesso cubo di riferimento], e dividiamo per 2 il numeratore del secondo rapporto, e sempre per 2 il denominatore del primo rapporto: otterremo il rapporto di 1/6, proprio quello dell’unghia cilindrica, quale termine occulto di connessione con il cilindro a croce.

Archimede ideò i due singolarissimi solidi delle proposizioni 14 e 15 del Metodo sapendo genialmente ciò che faceva e conoscendo già intuitivamente i risultati, salvo poi dimostrarli formalmente [ci è pervenuta nel palinsesto soltanto la dimostrazione formale per l’unghia cilindrica].

Adesso sappiamo anche che stava (in qualche modo) prendendo per i fondelli Eratostene che evidentemente se lo meritava.

LA MENTE PRODUTTIVA DI ARCHIMEDE

1* Scriveva il celebre matematico Piergorgio Odifreddi (La Repubblica 23 dicembre 1998) che dopo la lettura a raggi ultravioletti e a raggi x del palinsesto del Metodo finalmente “conosceremo come ragionava Archimede”.

Come “ragionava”Archimede? Più che alla “psicologia della Gestalt”, che pure sembra coinvolta, bisognerebbe rifarsi all’antico spirito di Pitagora o al moderno spirito di Einstein. Archimede conosceva l’arte degli esperimenti mentali. L’intelligenza umana ha sempre operato in questa maniera. Antico e moderno in ciò non sono distinguibili se non per circostanze accessorie.

I Matematici sono persone di grande valore, sanno bene ciò che dicono. Il mondo misterioso, tale è l’universo matematico, non è pero fatto di opinioni.

Qui non stiamo facendo matematica (non è nemmeno nelle nostre possibilità), ma stiamo ragionando intorno a ‘qualcosa’ che poi sarebbe il germe intuitivo del genio di Archimede. Come fisico e come grande matematico dell’antichità Archimede va lasciato agli Addetti ai lavori; la “questione archimedea”non pone problemi specialistici, bensì chiederebbe una soluzione. Così vanno letti questi appunti, senza creare confusioni indebite tra un settore specialistico e un giudizio valutativo. La scommessa fatta a suo tempo col Prof. Napolitani e col Prof. Acerbi, seri Studiosi di matematica antica, non può andare oltre i termini della questione. Tengo a precisarlo per evitare ogni frainteso. I miei ‘appunti’ non hanno valore scientifico e tuttavia non appartengono nemmeno al regno della fantasia. Occupano invece una frangia grigia, dove forse non è inutile un esercizio di finezza nella libertà d’indagine. Ed è in quest’ambito possiedono un loro valore e un loro significato, salvo errore.

Lo scrivente non conosce il calcolo infinitesimale e non può rendersi conto degli integrali che si riferiscono in generale al calcolo delle aree e dei volumi o al problema posto dal calcolo del perimetro dell’ellisse, a differenza della sua area (identità tra cerchio ed ellisse a tal riguardo). Ma trattandosi di altre questioni, elementari nella loro sostanza, non è un arbitrio parlarne. In specie se si cerca di interpretare alcuni eventi e alcuni fatti relazionali. Non saprei calcolare il problema bovino, ma posso intenderne alcune spiegazioni matematiche e alcune altre ‘modalità’. Del resto si tratta di un epigramma reco di 44 versi. Ciò riporta ancora una volta a Eratostene.

Eratostene, che non aveva saputo risolvere quei due problemi poi inseriti nel Metodo, si vede recapitare col trattato sul Metodo delle impeccabili soluzioni formali, tuttavia collocate in un impianto ‘sperimentale’ di geometria inusitata (quella della grandezza di Archimede che sapeva servirsi di mille risorse).

In realtà, Archimede continuava a nascondere i semi del suo genio.

La sorte di Eratostene è uguale alla nostra se non riusciamo a capire su quali invisibili intuizioni si sia fondato Archimede senza rivelarle nemmeno nel Metodo. La risposta sarebbe lo spirito della “scuola italica”, e non lo spirito di “Alessandria” dopo Euclide.

Archimede non aveva abbandonato Siracusa e non intendeva distaccarsene. Abbiamo scoperto un altro lato del suo carattere. Il barbuto effigiato i profilo nella medaglia Fields, ambito riconoscimento per i migliori matematici, era un uomo dal carattere forte, fiero, orgoglioso: un individuo vigoroso quanto il suo intelletto divino. Nelle Tuscolane Cicerone ricorda più volte Archimede. Il cavaliere di Arpino quando era questore in Sicilia ritenne di averne scoperta la tomba (di cui i siracusani addirittura negavano l’esistenza) nella zona della porta agrigentina. Nascosta tra i rovi, un’iscrizione recava alcuni versi (rovinati dal tempo e non riportati da Cicerone), in cui si parlava di una sfera e di un cilindro. Sopra una colonnina c’erano scolpiti una sfera e un cilindro. Erano forse un simbolo di immortalità, oltre che un richiamo alle opere del Siracusano?

2* La superficie sferica non è ‘stirabile’ su un piano. Lo impedisce la sua ‘curvità’ perfetta. Se fosse fatta di una sostanza materiale, bisognerebbe farla a striscioline infinitesime, eppure la superficie sferica corrisponde sempre a un’area determinata, all’area di 4 cerchi massimi di quella sfera di raggio dato. Nasce un problema. Finito e infinito sembrano coincidere. In realtà esistono ordini diversi d’infinito, come la matematica moderna ha posto in luce (l’infinito numerico dei numeri naturali è però equivalente all’infinito del quadrato di questi numeri).

Il piano delimitato, che come area ha dimensione 2, non può avere la stessa dimensione della superficie sferica. Quest’ultima, che racchiude il massimo volume solido, deve avere dimensione 4. La superficie sferica è sempre 4 volte l’area del cerchio massimo. Quale sia l’ampiezza del cerchio in funzione del raggio e quale sia dunque il volume della sfera. L’invariante pigreco è un numero trascendente.*[In matematica sono detti trascendenti in numeri reali o complessi che non siano radice di alcuna equazione algebrica a coefficienti razionali]. L’invariante 4 tipico della superficie sferica (che è poi un semplice numero naturale) deve avere qualcosa di misterioso, che nemmeno il calcolo infinitesimale spiega, se non come risultato. Questo numero corrisponde alla quarta dimensione. Rappresenta il valore 4 della dimensione del piano ideale infinito che è in grado di produrre la forma di ogni realtà fisica contornando la sfera del tutto, il rotondo Sfero dell’Essere. Il piano infinito è implicito nella geometria analitica di Cartesio e contiene tutti i numeri possibili, anche i numeri complessi (c.d. piano di Argand), con una capacità superiore a quella della c.d. retta numerica alla quale si ricorre per la rappresentazione dei numeri. Il concetto di numero è immateriale, i numeri figurati di Pitagora (numeri triangolari, numeri quadrati ecc.) trovavano la loro ‘rappresentabilità’ disposti su un piano tendenzialmente infinito (per esempio i numeri triangolari si collocano in un triangolo crescente, i numeri quadrati in aree quadrate crescenti).

Analogamente, possiamo notare che nella formula per il calcolo del volume della sfera compare il fattore 4/3, che è un puro rapporto numerico. “Quattro terzi di che cosa” se in questo caso non esiste un termine di paragone, diversamente dal fattore 4 della superficie sferica, che ha infatti riguardo a quattro volte l’area del cerchio massimo?

Questo termine di paragone però esiste, ma in modo occulto: ed è adesso la quarta dimensione rispetto alla terza. [Il matematico Serge Lang, spiegando ai ragazzi delle scuole medie di New York da dove vengono le formule scolastiche comunemente impiegate nelle scuole inferiori a proposito del cerchio e della sfera a prescindere dal moderno calcolo infinitesimale, avrebbe dimenticato un passaggio]⁴. L’invariante 4/3 della formula del volume della sfera è connesso a un’essenza dimensionale. Il piano ideale infinito, di dimensione 4, si è attualizzato nel volume della sfera in sé che esso racchiude. Il concetto è di una bellezza platonica. Il Demiurgo era un pitagorico. Divino l’intelletto di Archimede, pur costretto a utilizzare strategie umane. C’è nella realtà un mistero di ordine superiore, cioè una necessità astratta di potenza superiore che le forza in modo meraviglioso a essere in una data maniera, ma senza rinunciare all’Infinità e alla sublime Mente di Dio. Insomma la Bellezza, nella sinfonia dell’Essere. Finito e infinito si toccano come il dito di Dio e il dito di Adamo, nella Cappella Sistina affrescata da Michelangelo. Nella Poesia sperimentiamo dicibile e indicibile, come nella Matematica. Bellezza e Verità, un discorso infinito. E una conclusione di valore morale assoluto. Il dono di Dio non è tanto il capire, ma l’esserci (dasein in tedesco). La Bontà, il Sommo Bene (in Platone come anche in Cicerone), sono la Luce che i prigionieri della caverna avvertono. La contemplazione è Speranza.

3* Archimede conosceva già i risultati delle sue più elaborate dimostrazioni. Egli ragionava intuitivamente in termini di continuità dimensionale, cercando sistematicamente gli invarianti utili al suo scopo (la cui difficoltà era ben presente nel XVII secolo a Bonaventura Cavalieri, che ammoniva dal non trebbiar inutilepaglia).

Gli “indivisibili” di Cavalieri per una linea, sono i punti che la compongono; per una figura piana, i segmenti intercettati dalla figura piana; e per un solido, le sezioni piane del solido. Ad Archimede interessavano gli invarianti.

Gli indivisibili di Cavalieri erano implicitamente presupposti nell’opera di Archimede e poi testimoniati dal Metodo. Ciò non vuol dire che le opere di Archimede non siano come delle sinfonie, e che il canto della sua Sirena o della sua Musa domestica non fosse una melodia suggerita. Plutarco ha ragione anche in questo.

Piuttosto si dovrebbe presupporre che una copia del Metodo circolasse ancora all’epoca di Bonaventura Cavalieri, magari in un compendio arabo. Che fine avrebbe fatto? Il maggior indiziato è lo stesso Cavalieri che ne avrebbe estratto il metodo degli indivisibili. Il palinsesto del Metodo affiorò nel 1899, scoperto da un erudito greco, Kerameus Papadopulos, in antico messale proveniente da San Saba. Soltanto nel 1906 il celebre filologo danese J.H. Heiberg si accorse che era un testo perduto di Archimede. Heiberg fece eseguire la riproduzione fotografica del palinsesto, ricostruì il testo greco originale del codice che da un monaco era stato abraso con un raschietto e riscritto, e lo pubblicò. Soltanto in anni recenti, dopo le mille peripezie che l’originale aveva subito, sono cominciati studi ricostruttivi ricorrendo a tutte le tecnologie e competenze associate possibili.⁵ Si aveva conoscenza soltanto di due codici archimedei. Nel 1311, uno di questi codici che apparteneva alla biblioteca del Papa, sparì. L’altro codice appartenne al cardinale Ridolfi che muore nel 1560. Nel 1564 si persero le tracce anche di questo codice. Sappiamo che Leonardo da Vinci aveva dato la caccia alle opere di Archimede, quando in seguito pare che alcuni vecchi fogli di una qualche opera del Siracusano, secondo il matematico Tartaglia, erano stati usati da un salsicciaio di Verona per incartare la merce venduta al banco. *[Ovviamente esistevano delle copie, in mano a eruditi: Leonardo da Vinci ebbe modo di ricopiare una proposizione dal Trattato suigalleggianti, che trasferì nel Codice Atlantico]. Non si può escludere che il gesuita Bonaventura Cavalieri (1598 – 1647), un discepolo di Galileo a Pisa, la cui opera fu estesa dal Torricelli, avendo nominato l’unghia cilindrica, avesse letto o posseduto almeno qualche foglio del Metodo. Cavalieri è considerato uno dei predecessori dell’analisi infinitesimale che diverrà rigorosa agli inizi dell’800 mediante lo studio dei limiti. Il geometra gesuita si era roso conto delle difficoltà concettuali che l’infinito attuale comportava. Gli indivisibili gli consentivano di evitare errori concettuali compromettenti passando da una dimensione all’altra (linee, aree, volumi). La fama leggendaria e mitica di Archimede nell’immaginario odierno, anche di tipo scolastico ordinario, è esclusivamente legato alle sue invenzioni e non alla sua geometria, prevalendo in modo assoluto il nome di Euclide. Nulla di più falso,ma le opere di Archimede sono inusitate.

4* Ad Archimede non importava quanti ‘coni’ potesse contenere il suo ‘cilindro’ a croce. Questo calcolo non si poteva fare. Poteva essere stimato l’inverso: quanto volume del cubo, il cilindro a croce non era in grado di impegnare, data l’affinità del cono e con la piramide. In modo analogo furono affrontati i segreti del cerchio e della sfera.

Quanto al cerchio, la sua superficie poteva essere colta nel trasferimento all’area equivalente di un triangolo rettangolo. Quanto al suo perimetro, in una convergenza progressiva verso il cerchio dei lati sempre più piccoli dei poligoni regolari inscritti e circoscritti al cerchio.

Nella geometria di Archimede c’è indubbiamente il‘movimento’ della doppia convergenza verso un limite, come anche nella determinazione dell’area relativa della parabola. E così pure nella spirale.⁶

Si tratta di elementi necessari a un certo percorso, tipicamente archimedeo, anche se poi, da tali concetti, sono derivati – in nuce – i principi concettuali del calcolo infinitesimale. Se poi consideriamo anche l’altro aspetto, nascosto e ignorato, dell’intuizione dimensionale della geometria archimedea, da ciò si potrebbe ricavare l’idea di una possibilità di estensione di questi stessi concetti in altri campi. *[E’ nostra impressione, di cui però siamo incapaci di fornire elementi, che un percorso concettuale del genere possa condurre a risultati analoghi a quelli ottenuti algebricamente ad es. da Leibniz e da Wallis per derivare pigreco in successioni o serie numeriche].⁷

Archimede possedeva un’eccezionale intuizione e un talento straordinario. L’apparato dimostrativo di cui fa uso, tipico di un eccelso matematico che non lascia nulla al caso, ma che nella sua bravura intorbida le acque rispetto alle intuizioni di cui si è servito, non lascia trasparire d’onde gli provengano certe cognizioni già implicitamente presupposte, che sembrano dunque balzare dalla mente di Giove, come una Atena-Minerva armata. Neppure il Metodo lo spiegava.

I pitagorici avevano meditato sul rapporto tra geometria e numero, “computazione” babilonese e “geometrica egiziana”. L’arte babilonese del calcolo era chiamata logistica. I Greci preferivano la geometria. Archimede era un genio nei due rami.⁸

Il famoso teorema di Pitagora (che oggi si tende a sottrargli) rappresentava l’essenza geometrica del piano (come sosteneva Schopenhauer), e anche l’abile stratagemma per risolvere geometricamente l’irrazionalità del rapporto (in termini numerici) tra il lato e la diagonale del quadrato. Era un rimedio rivolto allo scopo, non di un segreto per cui Ippaso sarebbe stato ucciso dai pitagorici per averlo rivelato. Sono le leggende che oscurano la verità. I numeri quadrati servivano a connettere l’aritmetica con la geometria, collegando il discontinuo granulare dei numeri naturali col continuo geometrico che comprendeva i numeri irrazionali (l’alogos del rapporto tra lato e diagonale del quadrato).

Il quadrato costruito sull’ipotenusa equivaleva alla somma dei quadrati costruiti sui cateti. Ed era la proprietà stessa dello spazio piano.⁹ Il dramma del numero irrazionale, sorto in seno alla geometria, nella geometria si acquietava.

Il discreto numerico si appaiava al continuo geometrico. La tetraktys era il simbolo di tale unione. L’affermazione di Galileo essere i quadrati quanti i numeri naturali era già stata compresa dai pitagorici. Il discreto numerico si era trasferito nel continuo geometrico.

Per i pitagorici il reale era razionale. L’incommensurabilità delle diagonali rispetto al lato del quadrato era una virtù e non un abisso di perdizione.¹⁰ Alla stessa maniera il dramma di “pigreco” (un numero irrazionale e trascendente) si era acquietato con Archimede nei rapporti semplici del valore costante della superficie sferica e del volume della sfera e con le proposizioni 14 e 15 del Metodo. La stoffa del Cosmo era fatta di numeri naturali e di geometria. Dio non giocava dadi.¹¹ L’Universo poteva essere concepito come un rotondo Sfero.¹²

Il limite estremo o superficie di contorno del Cosmo sferico [come in certe rappresentazioni medievali: la testa di un uomo che vorrebbe sbucare oltre la sfera delle stelle fisse], era ugualmente finito e infinito, mentre il nulla è non essere.¹³

Il grande e il piccolo, il limitato e l’illimitato di Platone, sono sottintesi all’interno della concezione dello spazio geometrico e del numero, che aveva dato luogo al simbolo della tetraktys e ai numeri figurati pitagorici.¹⁴

Se tutti i corpi fisici sono rappresentabili da una geometria a 3 dimensioni, ciò non toglieva che il pensiero potesse concepire anche la dimensione “zero” del punto, senza cadere in contraddizioni. Il concetto di punto era l’astrazione geometrica del concetto di luogo, oppure di centro di gravità.¹⁵ Al limite estremo opposto si poneva la dimensione 4, rappresentata dall’invariante della superficie della sfera, estremo contorno del Cosmo a prescindere dalla sua grandezza.

La sfera e il cerchio infinitamente piccoli equivalevano a un punto geometrico senza dimensioni. Una fera infinitamente grande corrispondeva a un piano infinito (così riteneva il cardinale Nicolò Cusano nella Dotta ignoranza, opera famosa, composta come per un’illuminazione durante il viaggio di ritorno da Costantinopoli, nel 1437, dopo aver una missione diplomatica per conto del papa).¹⁶

A ben guardare, il pensiero cosmologico moderno non si è poi allontanato da questo scenario, a riprova della bontà teoria della conoscenza in Platone, che è fondata sulla reminiscenza (vedi ultimo libro della Repubblica e Menone).¹⁷

L’Universo della cosmologia moderna nasce da una singolarità iniziale a densità infinità e potrebbe anche espandersi all’infinito (modello piatto).

L’ultima fila della tetraktys rappresentava la realtà superiore. La tetraktys pitagorica non era un’effigie banale, ma un simbolo potente e arcano.

*[Le convinzioni sul pitagorismo professate di Augusto Renghini (nato a Firenze il 12 novembre 1878 e morto il primo luglio 1946 a Budrio: aveva fatto parte del futurismo e era stato membro del direttivo di “Lacerba”) non erano una gratuita bizzarria, anche se di Pitagora ci è giunta soltanto la leggenda.¹⁸ Renghini, nella sua opera inedita su Pitagora, si era occupato in generale dei metodi di analisi indeterminata per le equazioni di primo e di secondo grado, con alcuni casi particolari di terzo grado, e aveva trattato anche il caso specifico dell’equazione di Pell coinvolta nella risoluzione del complicatissimo “problema bovino”R di Archimede, la cui tipologia era stata già affrontata da Lagrange. Per passare poi, il Renghini, alla trattazione dei numeri pitagorici figurati (numeri triangolari, quadrati, poligonali, piramidali e poliedrici: si veda su Internet il link dell’Associazione Culturale Ignis)].¹⁹

5* Il volume della sfera esige l’invariante di 4/3 che rappresenta un altro rapporto ‘dimensionale’ ove 3 significa ‘dimensione solida’ e 4 significa il ‘piano infinito’ indistinguibile dalla superficie di una sfera infinita ma ugualmente proprio di ogni sfera con raggio determinato.²⁰ Sono questi gli esempi più calzanti dei numeri archimedei o rapporti semplici di cui a ragione parlava Attilio Frajese a proposito della questione archimedea. Napolitani, svilendo un po’ Frajese, ma scrivendo un bel saggio, non avrebbe scorto questi aspetti, eretici per uno storico della matematica, rinviando però ai primi articoli di Reviel Netz e di Ken Saito sulle proposizioni 14 e 15 del Metodo, pubblicati nel 2000 sulla rivista Sciamus.²¹

I due studiosi ragionavano da addetti ai lavori, mentre nella sua sostanza più elementare la questione sembra diversa. E lo sarebbe anche perché Archimede non conosceva il calcolo infinitesimale e non gli era mai passata in mente alcuna idea al riguardo, sebbene la radice delle questioni da lui trattate avesse molti punti in comune con i fondamenti del calcolo infinitesimale (almeno per quanto concerne il concetto di limite e quello di grandezza piccola a piacere).

Il calcolo infinitesimale moderno (di grande complessità nei suoi molteplici sviluppi) fornisce una spiegazione ‘operativa’ di questi rapporti dimensionali, che rimangono nell’ombra. Le serie o somme infinite di Wallis e di Leibniz per pigreco dovrebbero avere una loro intima ragione ‘dimensionale’ o qualcosa del genere. “Pigreco” è uno degli infiniti numeri trascendenti, ma era un rapporto di grande valore per la geometria antica e lo è anche per la fisica e la matematica moderne.²²

*[Se una serie o una somma infinita converge al limite di pigreco ciò non dipenderebbe da un fatto aritmetico, che non spiega altro che se stesso, ma potrebbe avere una ragione profonda. Per esempio, la formula in progressione aritmetica di Leinbinz-Eulero per la convergenza verso il valore di pigreco / 4, avrebbe natura ‘dimensionale’. Anche la funzione zeta di Riemann ‘appartiene’ all’universo simbolico della tetraktys pitagorica?].²³

Archimede non solo realizzava la sua matematica, ma la contemplava. Una mente come la sua poteva scorgere nel “grande serbatoio”, secondo quell’istinto sublime che caratterizza i grandi e che era la caratteristica naturale di un genio moderno come Ramanujan, devoto alla sua piccola dea Namagiri.

Nella mente umana (simile alla caverna di Platone?), una dea benevola ha posto una luce misteriosa che soltanto a pochi è dato scorgere con chiarezza Per questa ragione, tutto dedito alla sua Musa domestica, Archimede non apprezzava più di tanto le applicazioni tecniche, che si dovevano soltanto adeguare ai principi non potendoli mai superare, e che soprattutto non li spiegavano. La speculazione teorica è molto di più, sebbene anche di pane vive l’uomo. La scienza moderna è diversa. E’ operativa, non guarda mai alle cause ultime, non ha spessore “filosofico”, abiura la metafisica memore dei traviamenti aristotelici. Eppure il darvinismo è diventato una specie di metafisica col pretesto della sua scientificità. La scienza moderna ha i suoi limiti e i suoi vuoti. Prima di ogni cosa viene l’uomo, immerso nella natura. La nuova etica a ciò si appella, comunque incapace di abrogare Dio.²⁴

ANCORA SU ARCHIMEDE

1* Anche in fisica Archimede era alla ricerca di invarianti nel senso di ciò che non muta e perciò consente all’Essere di Parmenide di rimanere se stesso.²⁵ Egli tendeva a risolvere la dinamica nella statica. Se il mare è spesso tempestoso, tuttavia il suo moto alla fine si placa tendendo all’equilibrio. L’incessante e cieca agitazione degli atomi non impedisce all’Universo una scala di stabilità. Archimede non era un atomista epicureo, ma un pitagorico platonico. Il caos, fisico e matematico, tende alla fine a stabilizzarsi verso certi attrattori. La natura tende all’equilibrio. E’ la seconda legge della termodinamica, la legge dell’entropia, che viene a essere associata alla ‘morte’, mentre le leggi di conservazione hanno in fisica un grande valore. L’energia tende a disperdersi. L’agitazione molecolare si placa. Anche l’azione meccanica può essere diluita. Su questo si fonda il principio della leva. E con mano femminea le macchine di Archimede traevano a riva grandi navi.

Già al tempo di Archimede il fenomeno delle maree era stato collegato all’ influsso misterioso della luna. Gli alessandrini conoscevano questo effetto [lo sapevano empiricamente i marinai collegandolo intuitivamente con la luna] e si saranno domandati come ciò potesse accadere. Le maree erano studiate da Seleuco di Babilonia, nel mare Arabico e in quello Indiano.²⁶ Nel trattato Suigalleggianti Archimede fornisce una prova della sfericità della Terra.

La forza di gravità agisce verso il centro della Terra. Secondo il principio dell’idrostatica è implicata la forma sferica dei mari in condizioni di riposo. Questa spiegazione riguardava soltanto gli oceani, ma poteva essere estesa al pianeta. L’ipotesi di Archimede in condizioni di riposo fu contraddetta da Eratostene per la sua incompatibilità col fenomeno delle maree.

Il principio d’azione e di reazione è un genere di equilibrio, una legge di conservazione o un invariante. Archimede considerava le trasformazioni non in senso dinamico, evolutivo o irreversibile, come nell’entropia, ma nella direzione dell’equilibrio e della sintesi degli opposti.

La sua statica, che raccoglieva anche la meccanica, postulava i centri di gravità. E se agendo con una sola “femminea mano” si poteva tirare a riva una grande nave (come narrano Plutarco e Silio Italico), così smentendo Aristotele, che lo reputava impossibile, ciò esigeva che le trasformazioni reciproche del moto e delle forze fossero compensate dalla differenza dell’azione rispetto allo spazio percorso e al tempo (durata dell’azione). Era un invariante, di tipo fisico, sempre inserito nel regno concettuale dell’equilibrio statico. Archimede ignorava volutamente la dinamica. Quale forza muoveva le orbite planetarie, Luna compresa? Nell’Arenario c’è un riferimento all’ipotesi eliocentrica di Aristarco, con la Terra che compie un’orbita (circolare) intorno al Sole. Quindi, la terra ruota su se stessa, e il suo asse di rotazione deve essere inclinato dello stesso valore dell’inclinazione apparente dell’eclittica, per riuscire a spiegare le stagioni. Archimede, che era un genio, non poteva non essersi posto tali domande. Eppure nulla risulta, giacché ci sono giunte soltanto alcune delle sue opere. Ma sappiamo che costruì delle sfere celesti, e parrebbe anche che fossero di tipo diverso. Qual era la concezione cosmologica di Archimede, se nell’Arenario le dimensioni dell’Universo sono ampie? La parallasse stellare non era stimabile. Si trattava di oggetti lontanissimi. Archimede incerto su quale modello cosmologico accogliere, quello eliocentrico di Aristarco oppure quello geocentrico di Aristotele? Ad Aristarco muove un’obiezione debole, che conferma la grandezza del cosmo. La grandezza del cosmo, qui inteso però come sfera dei pianeti orbitanti intorno al Sole, stimata da Archimede è minore di una miriade di volte il diametro della Terra. Pertanto, anche il diametro della sfera delle stelle fisse (intero Universo) è meno di una miriade di volte ildiametro del cosmo (l’ipotesi assunta da Archimede era che la grandezza della sfera delle stelle fisse, oggetti assai lontani, rispetto alla sfera planetaria fosse nella stessa proporzione gerarchica della grandezza della sfera planetaria rispetto al diametro terrestre). Quanto valeva per Archimede il diametro della Terra misurato in stadi?²⁷ L’Arenario è il libro dei gradi numeri (ottadi). L’Universo di Archimede nell’Arenario (assumendo l’ipotesi eliocentrica di Aristarco, ma nel merito di tale ipotesi non pronunciandosi), è più piccolo dell’Universo postulato dal “problema bovino” capace di contenere mandrie infinite di 4 specie di tori e di vacche delle mandrie del Sole.²⁸

2* Il facile strumento della leva semplice, noto da millenni prima che Archimede se ne occupasse,²⁹ incorporava un principio della statica. La forza di resistenza e la durata dell’azione si compensavano e il risultato dello spostamento non proveniva misteriosamente dal nulla, ma era spiegabile e razionalizzabile come invariante. La leva semplice era comunemente impiegata in edilizia, come gli argani e le carrucole. Non solo le antiche Piramidi, ma anche i templi greci non avrebbero potuto essere costruiti, senza l’utilizzo di queste apparecchiature, che trovavano impiego anche per le costruzioni navali e le manovre di carico e di scarico delle merci. Archimede certamente non le inventò, ma le studiò e le perfezionò. La conoscenza esatta dei principi che vi presiedevano permetteva ampliamenti e nuove invenzioni.

Archimede impiegò le leggi della meccanica anche in chiave geometrica per “scoprire” teoremi di geometria.³⁰ In realtà, la fase intuitiva del pensieroproduttivo o trasformativo del Siracusano è precedente anche a tali esperimenti euristici, inseriti nel Metodo. La determinazione del volume dei conoidi esigeva una verifica meccanica, ma anche in questo caso l’idea primitiva aveva un carattere ‘dimensionale’

Ugualmente, era empiricamente noto, e come tale era utilizzato, anche l’effetto del galleggiamento, fondato sulla controspinta dell’acqua. I marinai esperti sapevano stimare a occhio il carico corretto e la dislocazione di sicurezza delle merci per una nave mercantile. Archimede spiegò perché e costruì una teoria anch’essa fondata su principi d’invarianza. Alla forza equivalente al peso del corpo immerso, il liquido rispondeva col suo peso specifico e la sua resistenza. E’ implicito che Archimede conoscesse il principio dei vasi comunicanti, attribuito a Erone, e forse conosceva anche il paradosso idrostatico di Pascal (il fatto che non ne parli, non o esclude automaticamente). Anzi era altresì implicito nel principio generale d’invarianza l’aumento della pressione se si restringe la sezione del condotto. La scienza archimedea era già una forma di scienza moderna, dove però il metodo deduttivo oscurava quello induttivo e sperimentale, com’è tipico dei sistemi assiomatici. Se poi Archimede avesse effettivamente ideato e costruito il primo telescopio a riflessione è questione poco nota, ancorché dubbia. Poteva averlo fatto, giacché il ritrovato era alla sua portata, specchi parabolici di bronzo e lente semplice, rientrando peraltro nei medesimi principi generali d’invarianza, giacché poteva essersi reso conto l’avvicinamento dell’immagine di un oggetto lontano avviene a discapito della sua luminosità (ed è un altro esempio d’invariante, applicato all’ottica).

La forza di gravità, pur così evidente nei suoi effetti, non costituì a quanto pare argomento di particolare d’attenzione nel mondo antico, anche se il piano inclinato (di non facile concezione) è un altro esempio d’invariante sperimentale, con un attrito trascurabile. La gravità agisce verso il basso, in direzione del centro della Terra. Archimede lo sapeva. Nel moto rotatorio la forza tangenziale, che è diretta a sottrarsi al vincolo, è equilibrata dalla forza attrattiva verso il centro (come nell’esempio comune della corda nella fionda). L’ipotesi eliocentrica di Aristarco, richiamata da Archimede nell’Arenario, presupponeva queste idee. Viceversa, nel modello opposto, con la Terra immobile al centro dell’Universo, cosa spingeva il sole e i pianeti a ruotarle intorno, in orbite fisse, ruotando anche l’immensa sfera delle stelle fisse che sorgevano e tramontavano? I greci erano scettici sulla natura della gravità. Non sapevano darsene una ragione. Se la gravità agiva a distanza, diretta verso il centro della terra, poteva supporsi che le orbite celesti continuassero a ruotare incessantemente, insensibili alla “gravità”, in virtù del principio di conservazione del moto uniforme (prima legge di Newton), che tuttavia è rettilineo? Lucrezio conosceva già il principio di relatività galileiana. La nave sembra ferma mentre è il panorama terrestre a scorrere via in senso opposto.

Non c’è ragione per ritenere che scienziati del calibro di Archimede non avessero messo in conto la conservazione del moto uniforme non contrastato da attriti o resistenze. Perciò, quale forza animava il cosmo ruotante, e come mai se era invece la terra a ruotare, allora le cose terrestri non erano scalzate via? E’ impossibile che dopo le teorie di Aristotele, smentito dalla meccanica di Archimede, non si parlasse di questi problemi.³¹

Marte, con i suoi apparenti occhielli, non seguiva un moto orbitale circolare e dunque furono introdotti epicicli e deferenti per giustificare l’ipotesi geocentrica *[l’astronomo Giovanni Schiaparelli notò una stretta analogia tra la decomposizione in serie di Fourier e lo sviluppo in epicicli]. Le esigenze pratiche, connesse sopratutto alla navigazione, rendevano indifferenti i due modelli astronomici. La gravità era interpretata come una tendenza naturale, diretta verso il basso, ed era identificata con la pesantezza. Gli alessandrini avevano a disposizione tutti gli strumenti di ricerca poi utilizzati da Galileo e conoscevano anche il metodo sperimentale di cui però diffidavano. Galileo, che col suo genio avrebbe tranquillamente potuto immaginare l’esperimento del pendolo di Foucault per provare la rotazione terrestre, però non lo fece. Ecco un esempio delle stranezze, quasi inspiegabili, della storia della scienza. Archimede era alle soglie del calcolo infinitesimale, ma in ogni caso egli non aveva lo strumento numerico per conseguirlo. I calcoli dei Greci erano molto diversi dei nostri calcoli aritmetici fondati sullo zero e la notazione posizionale delle cifre, introdotta dagli Arabi.

LA CORONA AUREA DEL RE GERONE E MOLTO ALTRO

1* La legge idrostatica sullo spostamento di pari volumi di liquido e sulla conseguente ‘spinta’ verso l’alto in rapporto ai pesi specifici, era dovuta alla ‘pesantezza’ dei corpi.³² Una palla di marmo o di ferro affondava più velocemente di una palla di uguale volume, ma di materiale più leggero, almeno fino al punto di stabilizzazione nella caduta in basso.

In un esperimento ideale, concepito nel vuoto, la gravità avrebbe agito in modo invariante sulla massa e sui volumi, se nei liquidi resistenti valeva il principio idrostatico. Quest’altro invariante era perfettamente concepibile dal genio di Archimede. Con questi esempi abbiamo cercato di indicare che i confini tra ‘antico’ e ‘moderno’ sono abbastanza labili, almeno nel senso che certe scoperte sono state probabilmente impedite da un habitus mentale preconcetto anziché da incapacità. Lo studio accurato delle sezioni coniche porta quasi subito a Keplero. I pitagorici erano stati i primi a ipotizzare un cosmo eliocentrico. Il dodecaedro lo rappresentava.³³ I 4 elementi, aria, acqua, terra e fuoco, erano rappresentati dagli altri solidi. Qui parliamo dell’acqua e del principio idrostratico, che con una ‘bilancetta’ di precisione permette di stabilire i pesi specifici dei corpi e degli elementi chimici.

Vitruvio ci ha tramandato l’episodio leggendario della corona d’oro massiccio del tiranno di Siracusa, Gerone II.³⁴ Il racconto di Vitruvio è un’invenzione scolastica derivante dalle applicazioni sul peso specifico dei corpi, equivalente all’individuazione della loro natura. E’ invece interessante il problema delle fonti di Vitruvio giacché subito dopo Archimede comincia a parlare di Arcjita di Taranto e di Eratostene a proposito del problema della “duplicazione del cubo” (a tale scopo Eratostene inventò il mesolabio).³⁵

2* Non tutto il ‘curvo’ era ‘quadrabile’ in base all’opera di Archimede. Si ribellava l’area del cerchio. Anche il perimetro dell’ellisse si rifiutava *[difatti il calcolo del perimetro dell’ellisse è assai difficile: Archimede ci avrà riflettuto, senza trovare una soluzione]. Non così per l’area dell’ellisse, che come Archimede dimostrò, è pareggiabile a quella del cerchio [l’ellisse è un cerchio schiacciato].

L’area dell’iperbole è invece “in eccesso” e non è quadrabile. Al contrario della parabola e della spirale, cui Archimede dedicò due distinte opere.

La quadratura della parabola, che dà luogo a un rapporto fisso di 4/3 rispetto all’area del triangolo inscritto, e di 2/3 rispetto al quadrato circoscritto, impegnò Archimede in un lavoro trasmesso a Dositeo, morto da poco Conone di Samo, che era l’unico degli amici rimasti ad Archimede. Si può intendere che Archimede, da giovane, era andato a studiare ad Alessandria, e qui aveva conosciuto il valentissimo Conone, pure lui grande astronomo e anche grande matematico.³⁶ La loro amicizia si tradusse in una stretta collaborazione, interrotta dalla morte precoce di Conone, avvenuta verso il 246 a.C.

I rapporti di Archimede col gruppo capeggiato da Conone non si erano mai interrotti. Poiché Conone era morto ancora giovane, che fine hanno fatto i lavori che Archimede gli inviava e viceversa? Si rischia che le opere rimaste di Archimede siano prevalentemente quelle composte in età matura, tranne il trattato sulla parabola. Ne deriverebbe che il trattato sulla sfera celeste, come la sua realizzazione pratica, fossero lavori giovanili, dopo il rientro a Siracusa dall’Egitto.

Nella prefazione al trattato sulla parabola Archimede spiega a Dositeo, allievo successore del maestro, com’è giunto al suo mirabolante risultato, con due metodi diversi: dapprima con considerazioni di tipo meccanico, quindi con ragionamenti geometrici.

Il metodo meccanico consisteva in valutazioni di statica, tese a scoprire ciò che sarebbe accaduto se lo spazio curvilineo della parabola e quello rettilineo del triangolo inscritto fossero idealmente pesati con una bilancia.

Il metodo geometrico si fondava invece su una serie progressiva di bisezioni decrescenti (1/4, 1/8, 1/16, 1/32 ecc.), verificando se questa serie dicotomica avesse un limite cui tendere. La somma di questa progressione risultava pari a 1 + 1/3, così che la somma di tutti questi triangoli, progressivamente ridotti e rimpiccioliti, è pari a 4/3 di quella del triangolo inscritto ovvero 2/3 del parallelogramma circoscritto.

Anche questo mirabolante risultato era già noto in anticipo ad Archimede. Ci era già arrivato intuitivamente, con considerazioni di tipo dimensionale, sempre fondate sul principio di continuità. La serie 1/2 – 2/3 è ‘fitta’ in termini ‘dimensionali’ ed è l’unica possibile in un piano bidimensionale, relativamente ai rapporti relativi tra l’area del triangolo, della parabola, del quadrato contenente: quindi il valore dell’area della parabola è superiore a quello del triangolo, che perciò vale 2/3 di quella del quadrato; ma l’area del triangolo è ovviamente inferiore a quella della parabola, che vale 4/3 rispetto ad essa.

La quadratura della parabola dipende da questi rapporti che non ammettono termini intermedi. Con un analogo sistema di serie convergenti Archimede aveva calcolato il perimetro del cerchio, servendosi di un poligono regolare, inscritto e circoscritto, partendo dall’esagono, sempre raddoppiando i lati, fino a 96 lati in tutto. Si può notare che il numero 96 deriva dal raddoppio dei lati dell’esagono per 4 volte consecutive. In questo modo Archimede riesce a dimostrare che il valore della circonferenza del cerchio di diametro unitario, cioè “pigreco”, è posta tra il limite inferiore di 3+10/71 e quello superiore di 3 +10/70. Il rapporto di 22/7 ci dà, con piccoli numeri, un valore approssimato di “pigreco” per il rapporto irrazionale e trascendente tra la circonferenza e il diametro di qualunque cerchio (altro invariante).

La cosa sorprendente è che il rapporto di 22/7, corrispondente al limite superiore di “pigreco”, rappresenta (non importa se non in modo omogeneo) al numeratore il valore del volume della sfera (che è 22 relativamente al cilindro 33), e al denominatore il valore 7 del volume dell’unghia cilindrica, relativamente al cubo 42, contenente il cilindro stesso.

La mente di Archimede inseguiva un solo segreto: quello dell’Essere. L’Essere è e non può mutare: altrimenti si dovrebbe ammettere il non essere. Dunque esistono le leggi di necessità dell’Essere. La logica binaria di Parmenide, vero o falso, ha permesso anche il computer (corrente passa, corrente non passa).

L’area del cerchio è uguale a quella di un triangolo rettangolo di cui uno dei lati è uguale al raggio del cerchio e di cui l’altro lato retto è uguale alla circonferenza del cerchio medesimo.

Questo teorema è dimostrabile visualmente, immaginando che la superficie del cerchio si ‘srotoli’, a partire dal raggio fino all’esaurimento del giro, ritrasferendosi nel triangolo rettangolo che termina nel suo vertice più acuto.

Lo stesso principio dello ‘srotolamento’ vale anche per la dimostrazione visuale che l’aera sottesa dalla curva cicloide è pari a 3 volte l’area del cerchio generatore (la dimostrazione formale, ovviamente diversa da quanto qui suggerito, è dovuta a Torricelli, un allievo di Galileo).

La cicloide non rientrò tra gli interessi geometrici di Archimede; ma l’idea della cicloide è riconnessa alla teoria degli epicicli.

Nella quadratura della parabola si deve partire intuitivamente dall’idea che un ramo di parabola non deborda, non è in eccesso oppure in difetto, rispetto al quadrato che la può contenere (i termini greci si riferiscono proprio a questo fatto).³⁷ Il ragionamento formalizzato da Archimede non corrisponde all’intuizione, ma alla dimostrazione. Tuttavia, se si considera il triangolo isoscele inscritto regolarmente in un quadrato, si potrà notare facilmente che la sua area è pari a ½ di quella del quadrato stesso, come abbiamo già detto.

La parabola, inscritta nel quadrato, eccede l’area del triangolo isoscele, ma è inferiore a quella del quadrato. Quanto vale il rapporto tra le rispettive aree: quella del quadrato, quella del triangolo isoscele, e quella intermedia della parabola?

Come abbiamo già detto, il problema è stato risolto da Archimede con una dimostrazione formalmente perfetta, raggiungendo il risultato che l’area della parabola è 4 /3 di quella del triangolo ed è 2/3 di quella del quadrato. A tale risultato si poteva pervenire intuitivamente, attraverso considerazioni di continuità ‘dimensionale’ tra linee e piani.

3* Anche l’area della spirale corrisponde a un’intuizione simile. La spirale – altra sua bellissima invenzione di tipo geometrico – anziché esser vista come una curva sul piano, può essere concepita dinamicamente facendo scorrere una punta – in moto uniforme – sulla superficie di un cono uniformemente ruotante, a partire dal vertice del cono e fino alla sua base (primo giro).

La proiezione piana di questi due moti genera una spirale come curva che si ravvolge intorno a se stessa allontanandosi costantemente da un centro e avvicinandosi indefinitamente a esso. La superficie della spirale descritta nella prima rotazione sta alla superficie del suo circolo di rotazione nel rapporto da 1/3.

Si tratta di un altro invariante geometrico di tipo dimensionale: come il volume del cono sta a quello del cilindro nel rapporto da 1/3, così anche il valore dell’area del cerchio, nel primo giro, sta nel rapporto di 1/3 rispetto alla superficie della spirale. Si mantiene, cioè, nello stesso ordin, pur scalando di una dimensione.

La spirale è figlia del cono, come l’elica di Platone era figlia del cilindro. Nei successivi giri i rapporti mutano da 7 a 12, da 19 a 27 ecc.

Archimede riempie tutti gli spazi concettuali con una serie di teoremi, di proposizioni e di corollari: ma i principi ispiratori sono identici. Si tratta sempre delle proprietà dimensionali condivise dal ‘retto’ e dal ‘curvo’.

Archime concepì la spirale in modo cinematico, nella maniera seguente: una retta che ha un’estremità fissata, ruota uniformemente; su di essa si muove di moto uniforme un punto. La curva descritta sul piano da questo punto, sarà una spirale. Ma è la stessa cosa vederla nascere dallo scorrimento uniforme di una punta sulla superficie laterale di un cono, uniformemente ruotante.

Ancora una volta Archimede non ha rivelato la genesi intuitiva delle sue ricerche, ma le ha formalizzate stupendamente, come in un parto divino senza doglie.

Altro risultato importante a proposito della spirale è che dopo una rivoluzione completa il segmento di perpendicolare compreso fra il centro di rotazione e il punto d’intersezione fra la perpendicolare e la tangente, è uguale alla circonferenza del “primo cerchio”.

In altre parole, si mantiene l’invariante rotazionale, giacché ciò è dovuto al moto uniforme. Quando poi si tira la tangente alla spirale nella prima rotazione completa o primo giro, il punto d’intersezione con la perpendicolare dal centro di rotazione individua un percorso pari alla rotazione stessa: il cerchio ha dunque, come raggio, il segmento compreso fra il centro di rotazione e il punto di tangenza (Sp. proposizione 18). Ecco perché la spirale è correlabile a “pigreco”: altro meraviglioso risultato conseguito da Archimede che sicuramente aveva già intuito in anticipo. Per cui guardando alle sue opere riesce difficile stabilirne la cronologia, nel seno di che cosa preceda cosa.

E’ difficile credere che i falsi teoremi, che qualche volta aveva inviato a certi matematici alessandrini, fossero invece la conseguenza spiacevole di un suo errore. Si deve invece ritenere che lo avesse fatto apposta, ovviamente per uno scopo facilmente immaginabile: per una presa in giro.

Il trattato sulle spirali era stato inviato a Dositeo con la premessa che certi teoremi già trasmessi a Conone, si trovavano in massima parte anche nei libri inviati in passato allo stesso Dositeo tramite un certo Eraclide.³⁸ Conone doveva già essere morto da tempo e si deve anche intendere che tra Archimede e Dositeo c’era una speciale relazione, precedentemente alla morte di Conone, successiva all’anno 246. Anche Dositeo riscuote fiducia.

Il libro delle spirali inviato a Dositeo contiene adesso altre dimostrazioni nel senso che un conto sono le enunciazioni e altra cosa le dimostrazioni perfette e compiute. Le enunciazioni già inviate a Conone andavano risolte interpretate, ma Conone è morto senza avere avuto il tempo di affrontarle.

Archimede aveva grande stima di Conone. I due collaboravano intensamente, anche da lontano. Quei teoremi nessuno li aveva risolti. Era necessario dimostrarli.

Dopo la morte di Conone, Archimede aveva prodotto due falsi teoremi, a mo’ di sfida per quei boriosi matematici alessandrini che si vantano di cose che non sapevano risolvere o assurdità del genere. Eraclide aveva già recapitato a Dositeo le dimostrazioni esatte di Archimede intorno a certi altri problemi. Archimede indica a questo punto, a Dositeo, quali teoremi erano volutamente falsi. Poi Archimede passa a esporre alcuni problemi intorno ai conoidi di cui però non ha ancora inviato le dimostrazioni. Seguono le proposizioni intorno alla linea spirale, problemi che sono chiaramente d’altro genere.

Le dimostrazioni sulla tangente della spirale sono, poi, le più difficili tra gli scritti di Archimede. Molti matematici dubitarono di saperle comprendere e sospettarono persino degli errori. Il calcolo infinitesimale ne provò l’esattezza delle dimostrazioni.

Le notizie occasionali, presenti nelle premesse ai trattati di Archimede inviati ad Alessandria, contengono risvolti di estremo interesse, sui quali torneremo.

IL VOLUME DEL PARABOLOIDE DI ROTAZIONE

1* Tralasciando il trattato Sui conoidi e gli sferoidi, che impegna anche i centri di gravità e in cui tra l’altro si dà la dimostrazione non facile né scontata che il rapporto tra il volume del cilindro e quello del paraboloide di rotazione è pari a ½, si può tuttavia tornare a riflettere sul fatto se il Metodo meccanico spieghi euristicamente in quale maniera agiva Archimede per accostarsi ai suoi risultati, in seguito oggetto di rigorose dimostrazioni. Il Metodo è sufficiente allo scopo? La risposta è che il Metodo non risolve integralmente la questione. Gli indivisibili di Cavalieri erano impliciti alle presupposte “intuizioni” di Archimede, che nelle sue opere continua a indagare sulle proprietà dei suoi oggetti geometrici (aree, volumi, centri di gravità ecc.).

L’enunciato principale sul paraboloide di rotazione è che il suo volume equivale a 1/2 del volume del corrispondente cilindro, in cui si trova iscritto. A questo risultato si perviene valutando anche i centri di gravità. Archimede era perfettamente consapevole del rischio concettuale cui andavano incontro gli indivisibili. Il metodo meccanico, che sembrerebbe la prova, era invece una riprova, cioè un mezzo di controllo. L’intuizione era alla base della geometria archimedea. Forniamo un’altra spiegazione affine per il volume del paraboloide rispetto al cilindro.

Se il valore dell’area della parabola vale 2/3 rispetto a quella del quadrato entro cui il ramo di parabola è contenuto, poiché il cilindro inscritto in un cubo è, in sezione, equivalente come figura a un quadrato, allora la sezione verticale del paraboloide inscritto nel cilindro denota lo stesso rapporto tra la parabola e il quadrato circoscritto che sappiamo già essere equivalente a 2/3 dell’area del quadrato, mentre la sezione verticale di un cono inscritto in un cilindro vale in termini di superficie 1/2 e in termini solidi 1/3.

Pertanto, il paraboloide di rotazione vale, in termini solidi, 3/2 del cono, e se il volume del cilindro che è 3 volte quello del cono, allora il volume del paraboloide di rotazione vale 1/2 rispetto al volume del cilindro che lo contiene, dal momento che 3/2 moltiplicato per 1/3 fa 3/6, e cioè 1/2 .

Anche nel Metodo meccanico, diretto a Eratostene, è implicitamente presente l’intuizione pitagorica che però Archimede non rivela. Se l’avesse fatto, si sarebbe spogliato del suo “segreto”. Il Metodo non svelava a Eratostene nulladi eccezionale.

2* La geometria del XVII secolo – con Luca Valerio, Bonaventura Cavalieri, Galileo Galieli, Keplero, Torricelli e Pierre de Fermat – ripercorrerà la geometria di Archimede, ampliandola. L’antico maestro presagito da Platone aveva aperto la via che condurrà al calcolo infinitesimale, quando il numero, attraverso i suoi nuovi simboli, ignoti ai Greci, saprà fare a meno del disegno e della figura, cioè dell’intuizione e dell’idea visiva. Così è nata la matematica moderna, affrancata da ogni condizionamento esterno.

Il metodo per esaustione, che Archimede aveva ripreso da Eudosso e che era fondato sul concetto di grandezza piccola a piacere e sulla tendenza di due serie opposte a incontrarsi ovvero di convergere a un limite comune, non era l’anticipazione del principi del calcolo infinitesimale, bensì un passo obbligato del pensiero matematico verso la geometria del movimento, che Archimede aveva compiuto per altre ragioni. Il punto di contatto era dato esclusivamente dalla materia trattata, i segreti del curvo, che in generale esige l’impiego del calcolo infinitesimale.

Integrali e derivate, cioè le operazioni litiche e tetiche, tra loro corrispondenti, che compongono il calcolo infinitesimale, non appartenevano alla ricerca del Siracusano e neppure alle sue prodigiose intuizioni.

Archimede pitagorico ragionava in altri termini, non possedeva strumenti concettuali accostabili al “calcolo sublime”. Eppure l’armamentario della sua formidabile intuizione geometrica era in qualche modo già vicino ai primi rudimenti del calcolo infinitesimale che richiede tuttavia l’impiego delle cifre arabe e una metodica computazionale completamente diversa dal sistema di calcolo utilizzato dai greci, che anche per questa ragione trovava nella geometria uno sfogo necessario capace di rappresentare la realtà, mentre l’aritmetica non ne restava pregiudicata, e con essa anche la teoria dei numeri che ha sicuramente origini antiche. *[L’infinità dei numeri primi era stata dimostrata da Euclide].

I greci utilizzarono l’occhio e la mente in modo artistico, sopra l’abisso che i loro bianchi marmi esorcizzavano, dimentichi della morte nel Mondo delle Idee, rivolti al cielo immenso e incombente dei naviganti, il greco mare rosso-violaceo d’Omero. Nella contemplazione dell’Iperuranio e nei misteri del Demiurgo spaziava la loro anima creativa. Non era un atteggiamento prescientifico, vanamente metafisico. Contemplavano la Mente di Dio, come aveva compreso il maestro di Permenide, il profugo di Colofone Senofane, fondatore della scuola eleatica. Il mondo – secondo Senofane – coincideva con una divinità unica, eterna e immutabile. Lo stesso Dio di Einstein. Nulla a che vedere con l’atomismo epicureo, se si vuole intendere fino in fondo il paragone. E così era per Archimede, mente divina, come già indicava il suo stesso nome. Archimede astronomo, figlio di un altro astronomo pitagorico di Siracusa, Fitia o Fidia, che aveva studiato il cielo delle stelle fisse e i rapporti di grandezza tra la luna, la terra e il sole servendosi di strumenti molto semplici, al momento del sorgere del sole all’alba. Archimede aveva appreso dal padre i rudimenti della matematica e dell’astronomia, e nell’Arenario ne affiora il ricordo scientifico. Fidia aveva stimato la grandezza del sole.

E’ a questa fase giovanile che dovrebbe rimontare il perduto trattato sulla costruzione delle sfere celesti e l’effettiva costruzione di una p più di queste, o planetari, che dovevano adornare un tempio di Siracusa.

La sfera celeste di Archimede fu depredata dai Romani nel sacco della città e portata a Roma. Segno evidente della sua importanza e del suo grande valore. Occorre perciò parlare anche di Archimede astronomo. In quest’ambito esploreremo su basi indiziarie la possibile storia del telescopio e del cannocchiale 18-19 secoli prima di Galileo e di Newton. Una storia del possibile e non dell’impossibile. Una ‘storia’ che gli addetti hanno sempre avuto il timore d’affrontare per un eccessivo rispetto della storia moderna, ma la “sfera celeste” di Archimede basterebbe da sola a fugare.

Simili congegni tornarono in auge nel secolo dei lumi (cfr. M. Losano, Storie di automi – dalla Grecia classica alla Belle Epoque, Einaudi, 1990; B. Gille, Storiadelle tecniche, Editori Riuniti, 1985). Non sarà una novità, ma un aggiornamento. L’età moderna decollò sulla pista preparata dall’antichità. In mezzo, le crude vicende della storia, che avvilirono i secoli.

*Il seguito su Archimede nella parte terza dei nostri ‘appunti’.

(avv. Arcangelo Papi, febbraio 2014)

Bibliografia essenziale su Archimede:

• Pier Daniele Napolitani, Archimede, Quaderno n. 21 de Le Scienze, 2001;

• R. Netz e W. Noel, Il codice perduto di Archimede, RCS Libri 2007;

• P. Midolo, Archimede e il suo tempo, 1912, r. 1989, A. Lombardi Editore;

• G. Loria, Le scienze esatte nell’antica Grecia, 1913, r. Hoepli;

• L. Russo, La rivoluzione dimenticata, Feltrinelli I, 1997;

• M. Kline, Storia del pensiero matematico, vol. I, Einaudi 1999;

• C. Boyer, Storia della matematica, Mondadori 1980.